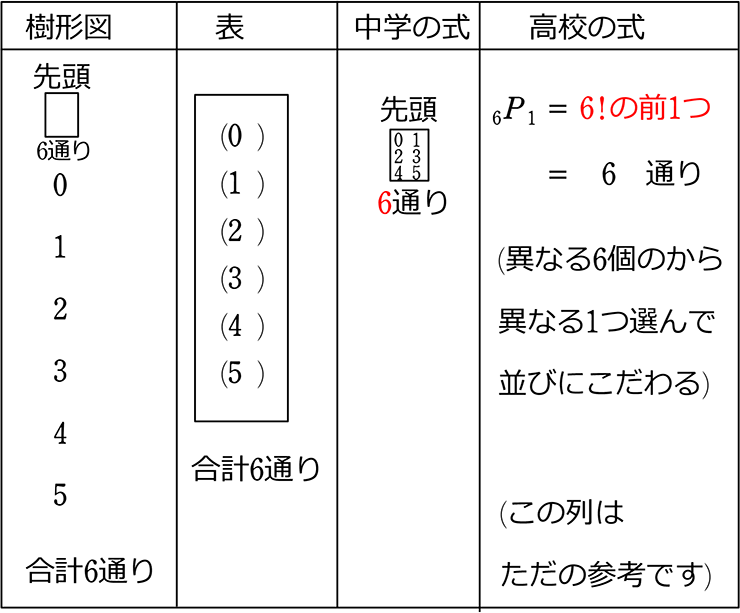
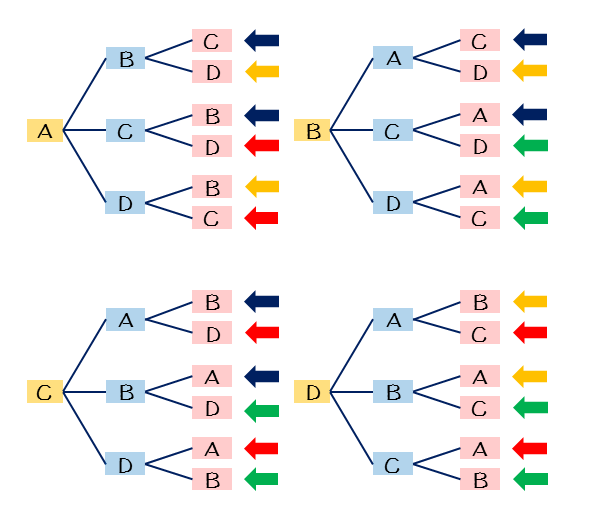
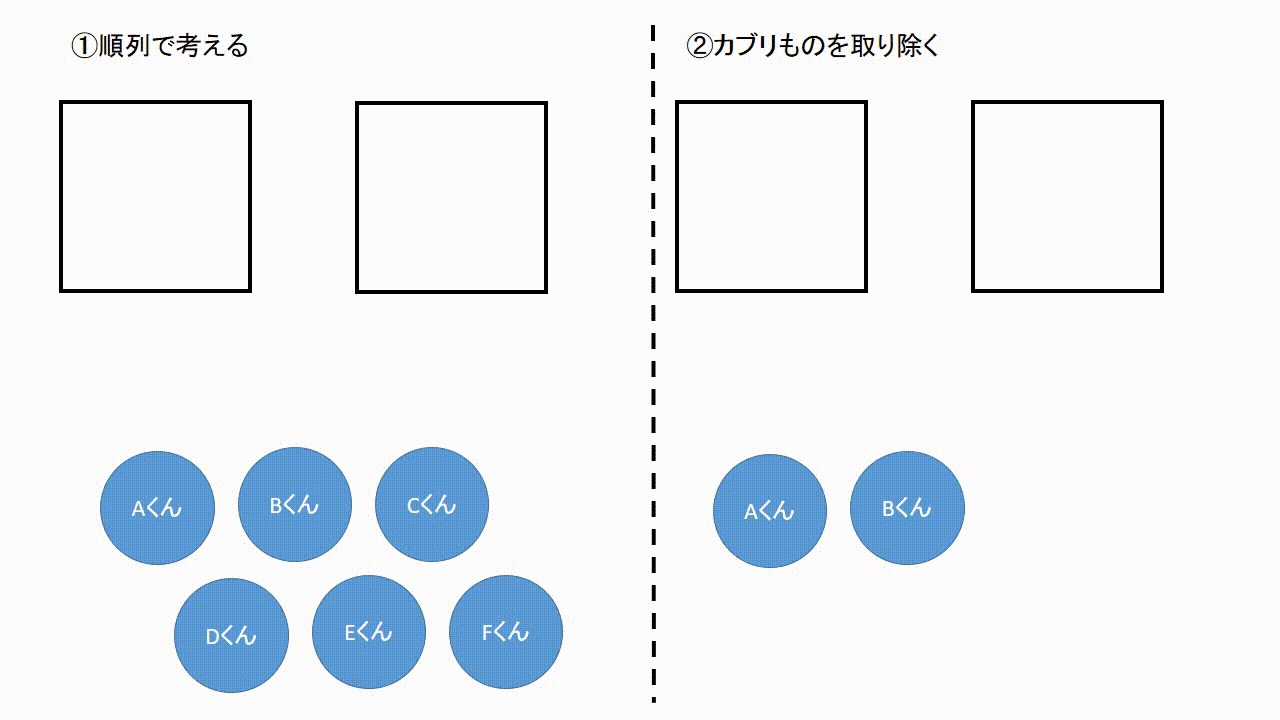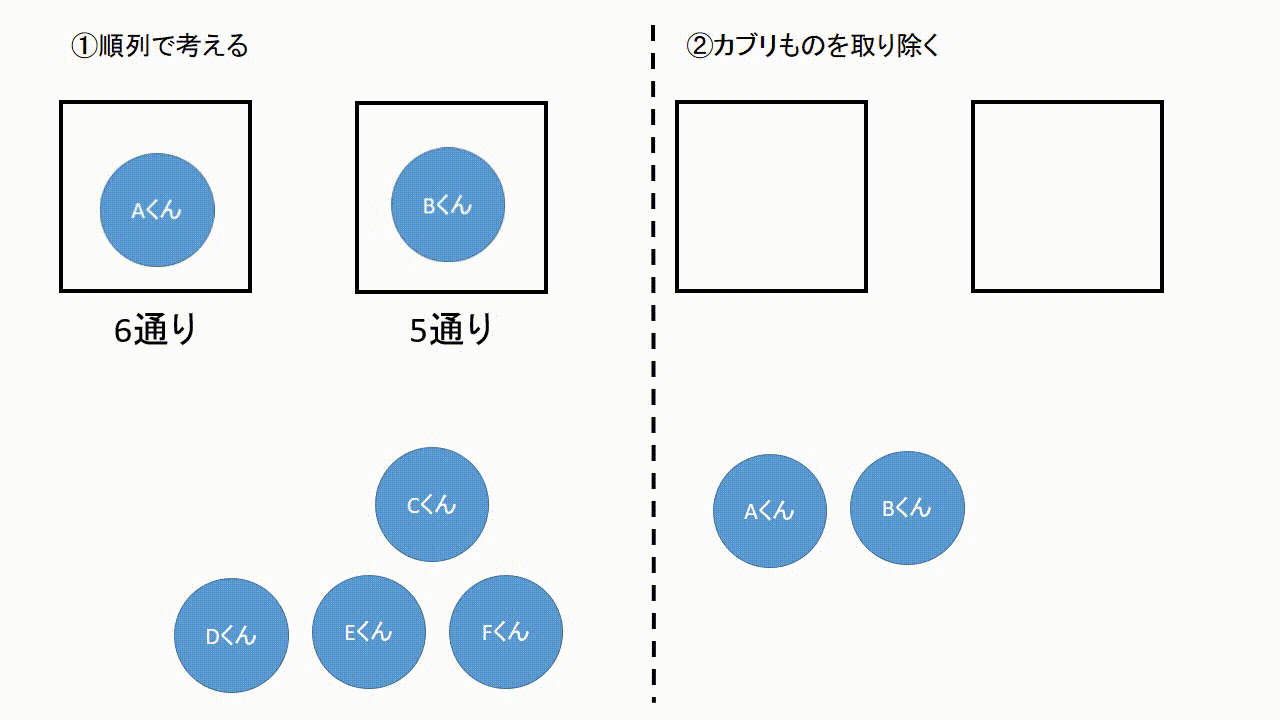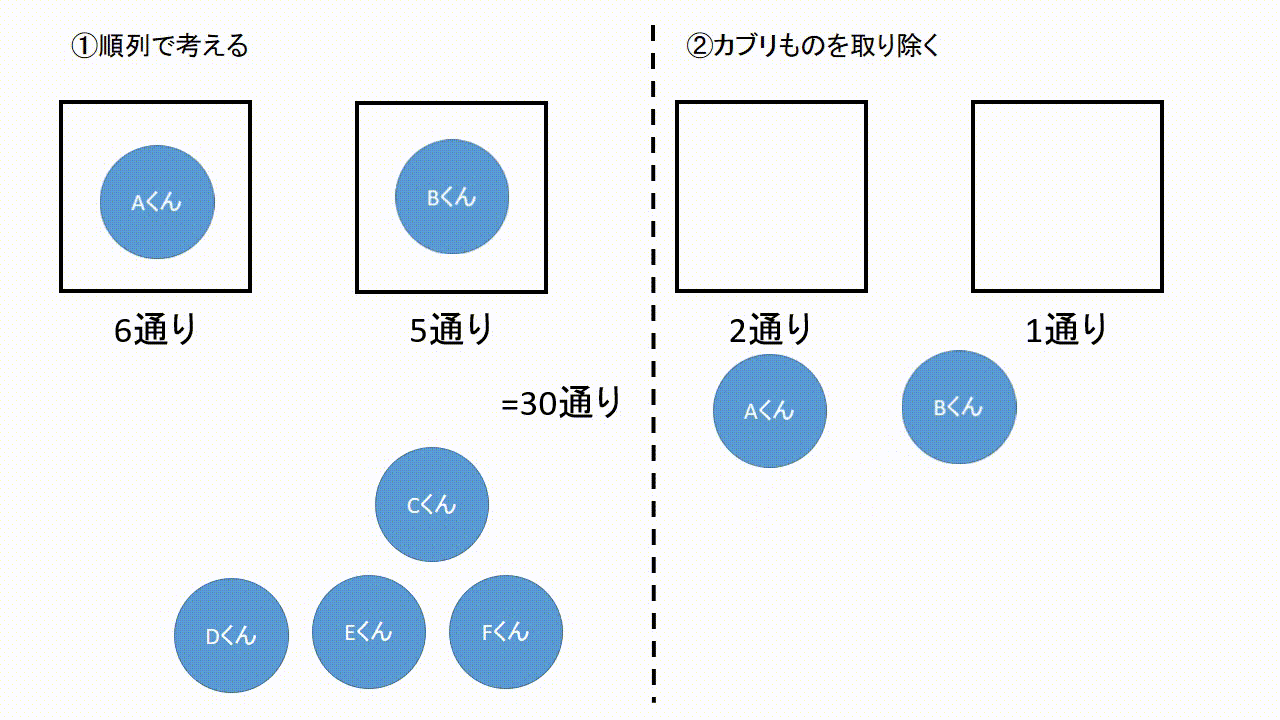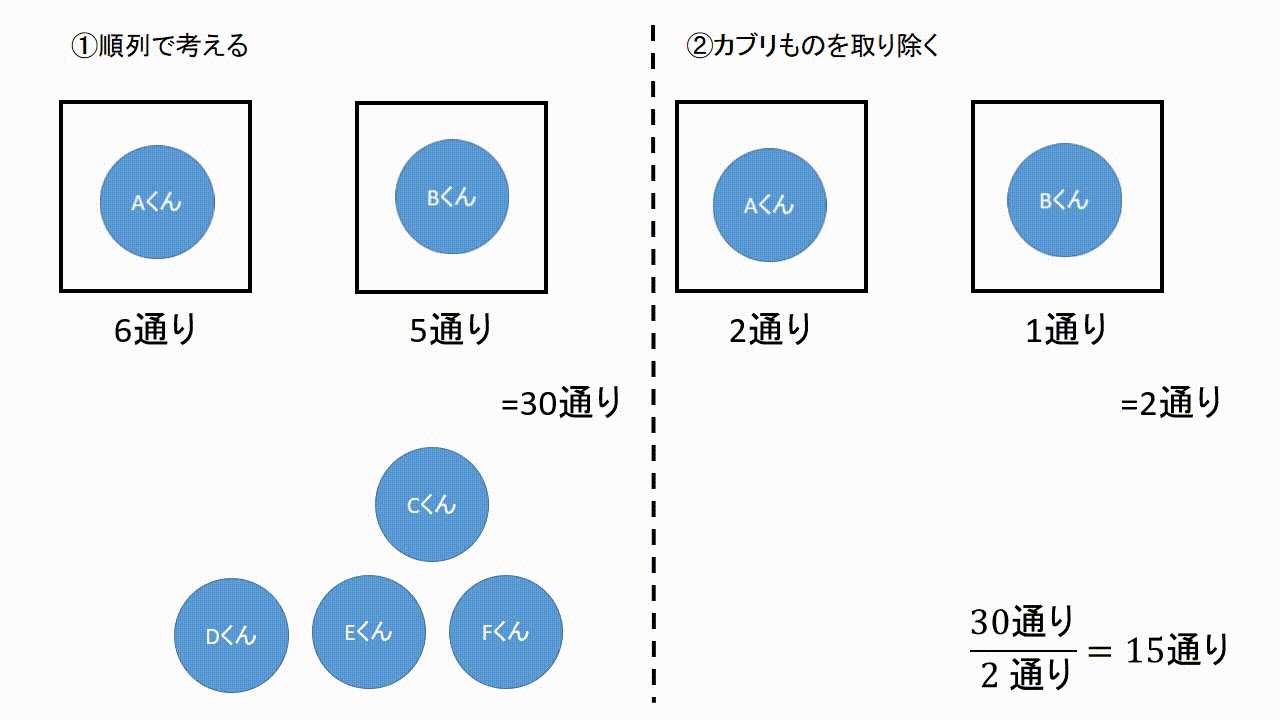
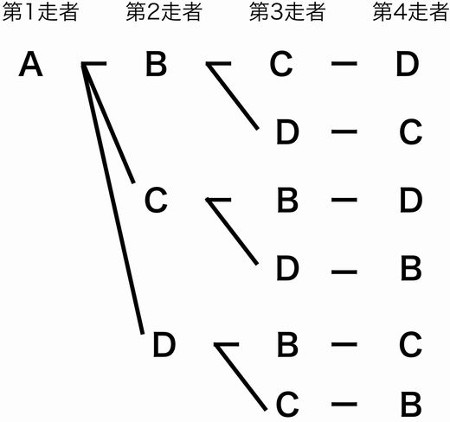
この記事では「順列」と「組み合わせ」の違いや見分け方について、公式や計算問題を通してできるだけわかりやすく解説していきます。 この \\(2\\) つはよく混同されるので、この記事を通してしっかりマスターしてくださいね! のようにACDの中で並べ方まで考えると明らかにそのパターン数は増えます。 ですから 「並べる」まで含めると場合の数はこの A C D のパターンだけで6通りになる わけです。 「選んで並べる」場合は順列の公式を私たちは知っていますから 5 P 3 = 5 ⋅ 4 ⋅ 3今回から 「順列」の場合の数 について学習しよう。 「順列」とは、漢字が表す通り 「順番をつけて並べる」 ということ。順番をつけて並べる場合の数 は、とても重要なテーマで、様々なパターンの問題があるんだ。 これから計10回にわたって、順列の問題のパターン別解法を説明していくよ。
中学数学 場合の数
場合の数 組み合わせ 違い
場合の数 組み合わせ 違い-「場合の数と確率」q&a一覧 場合の数と確率a∩b全体に ̄がつく集合 場合の数と確率a ̄∪bの図 場合の数と確率∪と∩の違い 場合の数と確率「どちらか一方」と「少なくとも一方」 場合の数と確率「同様に確からしい」の意味前回 https//wwwyoutubecom/watch?v=tpOLtMx_Bfk 次回 https//wwwyoutubecom/watch?v=pq3pJVNZrIU&index=15&list=PLKRhhk0lEyzPV58dAXzmfZle_wg03CLhl




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
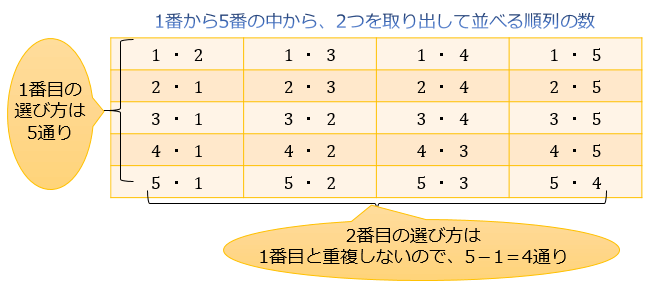
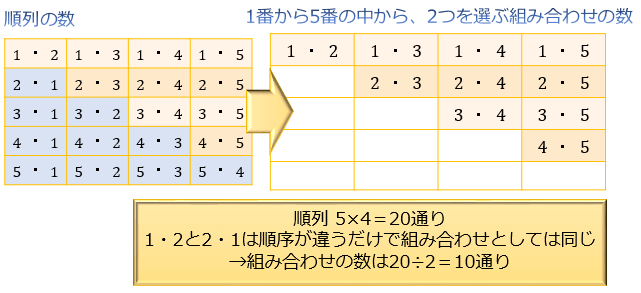
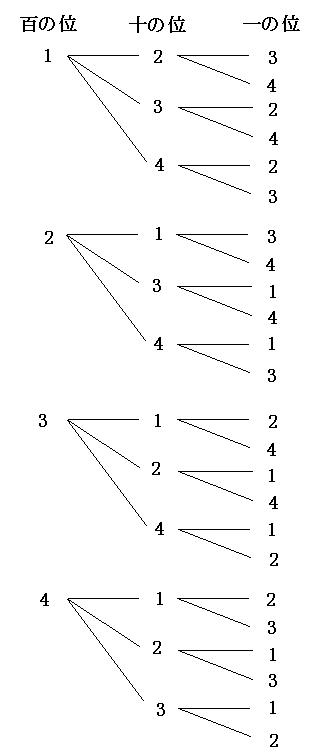
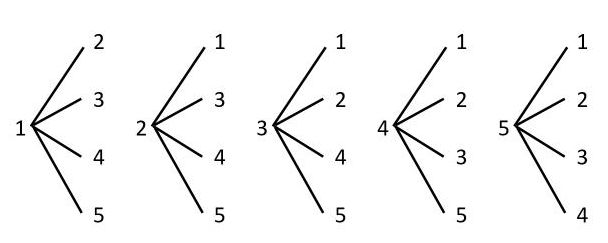
確率とは、場合の数を分数にしたものです。 しかし、実際の計算では、 単純に分数にしただけでは間違っている場合 があります。 例えば、本の中に当たりが2本入ったくじを考えてみましょう。 この中からどれか1本を引くとき、くじの出方(場合の数 (1) 5 5 5 人の中から 2 2 2 人代表を選ぶ方法の数を求めよ。 (2) 5 5 5 人の中からリーダーと副リーダーを選ぶ方法の数を求めよ。 (3) 3 3 3 桁の正の整数で各桁の数字が 0 0 0 でなくて全て異なるものはいくつあるか。 (4) 47 47 47 都道府県から 5 5 5 つ選ぶ場合の数は 単純な順列の 1 通りのうち、適当な 5 通りを選ぶと、このように重複する組み合わせを選ぶことができます。 これが「単純な順列を考えて、そのあと重複する場合の数で割る」という考え方です。 この「 5 」という数がでてきたのは、 5 人で順列を考えたからです。
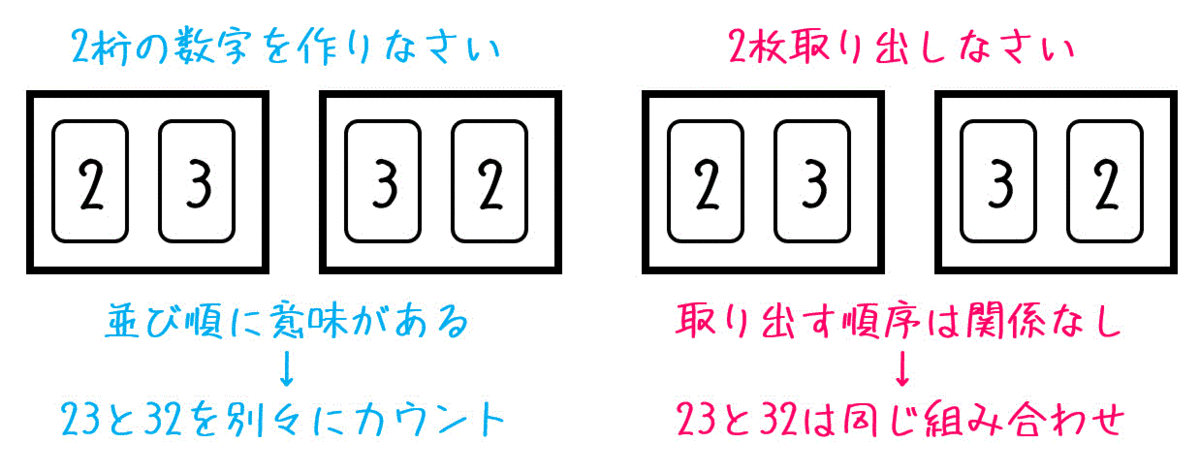
順列と組み合わせ ここでは、順列と組み合わせの違いについて、できるだけわかりやすく説明していきます。 で計算をする順列と、 で計算をする組み合わせ。 この使い分けに迷っている人も多いでしょう。具体的にそれぞれの計算式が使われる「場合の数と確率」q&a一覧 場合の数と確率a∩b全体に ̄がつく集合 場合の数と確率a ̄∪bの図 場合の数と確率∪と∩の違い 場合の数と確率「どちらか一方」と「少なくとも一方」 場合の数と確率「同様に確からしい」の意味 グループ分けで明確にしておきたい2つのこと これまでに 順列 と 組合せ について学習しました。 順列 は選ぶだけでなく 並べ方 まで考慮した場合の数で、 組合せ は 選び方だけ を考慮した場合の数でした。 単純な順列や組合せであれば間違うことはないかもしれませんが、 グループ分け
こんにちは、ももやまです。 今回は、 中学入試 高校入試 共通テスト(大学入試) spi(就職試験) 基本情報 など、様々な場面で出てくる場合の数、特に「順列と組み合わせの違い」に注目して説明していき 考え方を理解しよう!!あうるさん これまでに順列,組合せ,重複順列,重複組み合わせを学習してきましたが,今日はその使い分けについてです。 公式は全部使えるつもりだよ。 一つ一つの公式が使えるという前提で,どういう問題にどの公式を使えばいいか場合の数部屋割りの考え方についてイチから解説! 場合の数と確率 51 順列3桁、4桁の整数をつくる問題をパターン別に解説!




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート
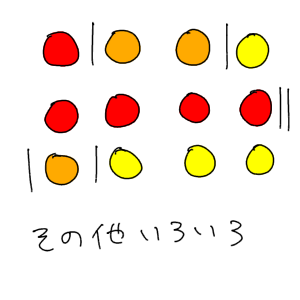



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書
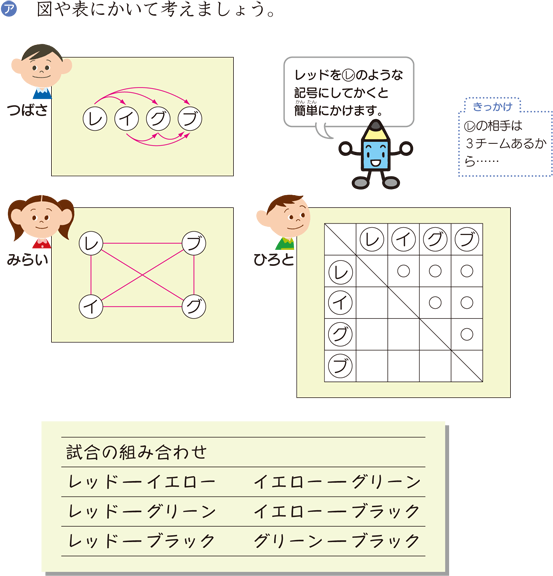
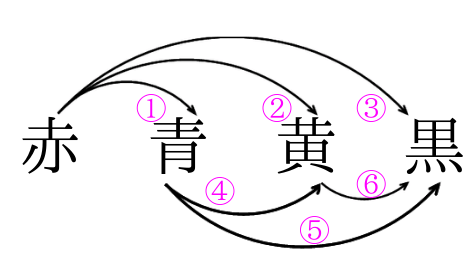
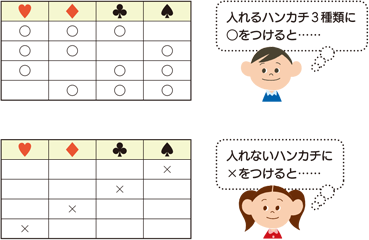
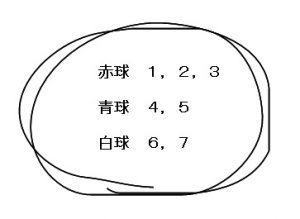
あとは引いた線の数を数えると6本なので、答えは6通りとなります。 組み合わせの数え方③表を使った数え方 表を下のように書きます。 まずは赤を必ず選ぶ場合を考えます。 赤の部分に丸印をいれます。 次に右隣の青にも印を入れます。順列、組み合わせ、円、重複、組分け。これらの場合の数の違いとその見分け方を簡単に解説します。 ここでは共通の例として、7個のガラス玉があった場合を考えてみます。 順列 7個のガラス玉から3個選んで一列に並べる $_7p_3$ 組み合わせ場合の数③ 組合せ 順列と組合せ 実は、ここまで学習してきた場合の数は、全て「順列」と呼ばれるものでした。このページでは「組合せ」について学習していきます。 では、順列と組合せはどこが違う




高校数学a 組分け問題全パターン 受験の月




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
10個の小石を3人に分配するとき、次の場合何通りの分け方があるか。小石はそれぞれ区別しない。 (1) 1個ももらわない人がいてもよい場合。 (2) どの人も1個以上はもらう場合。 (3) 人の区別をせず10個の小石を3グループに分ける場合。場合の数 高校の時の「 3 P 2 」とか「 3 C 2 」を覚えてますか? 公式はとてもカンタンなので、 完全に忘れていても30秒で覚えられます。 忘れている方 ⇒ 最速解法と例題 覚えている方は腕試し! ⇒ 問題11(組み合わせ) 重複組み合わせの公式がどのようにして得られるのかを紹介しておきます。 「\(n\) 種類のものから重複を許して \(r\) 個選ぶ方法」は、「\(r\) 個のモノと \((n − 1)\) 個の仕切りを一列に並べる方法」と同じ場合の数になります。



順列 P と組み合わせ C の違いって何ですか 数学1a 場合の数 Youtube




高校数学a 組合せの活用4 少なくとも 映像授業のtry It トライイット
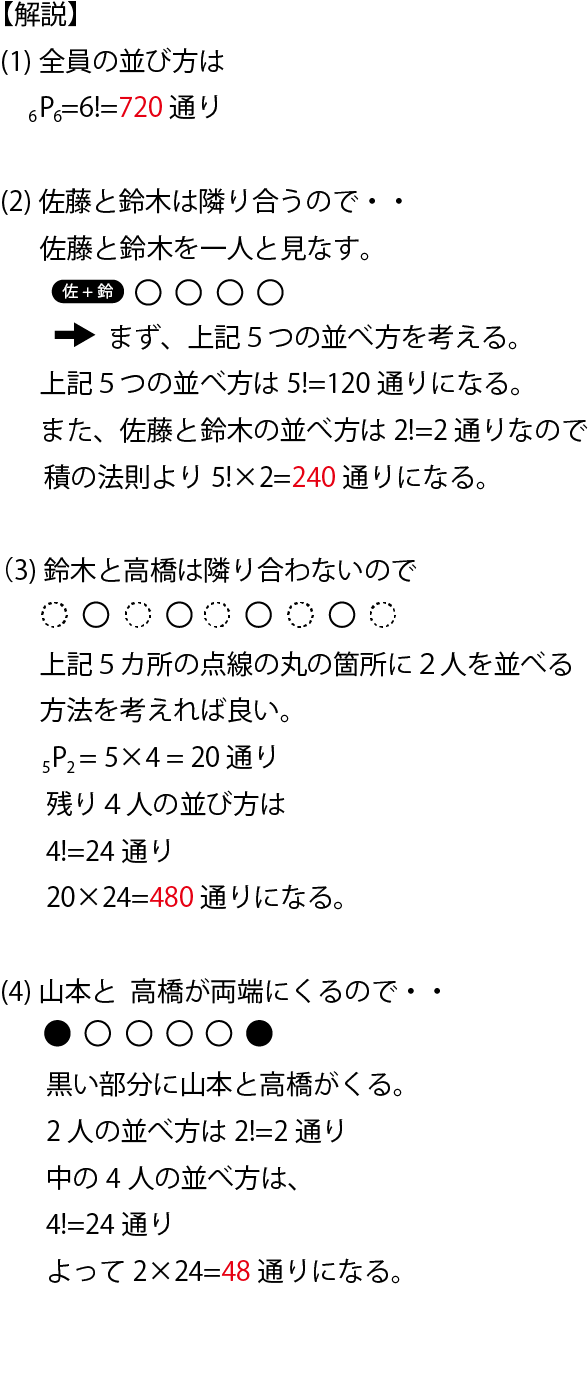
場合の数4| 組み合わせのnCrの求め方から性質まで攻略 前々回の記事では,「 n 個のものから r 個選んで並べる場合の数」である順列について説明しました. 「モノを選びとること」を組み合わせといい,「 n 個のものから r 個選ぶ場合の数」を n C r でāC ̖{ ɖ߂ ƁC ނ 10 Ԃ̖ ł͐Ԃ P ɂȂ Ă āC Œ肷 Ǝc ̂ ̂͒P ɓ ̂ Ƃ ̏ ɂȂ ̂ʼn ̂ł D ɑ āC ʂR C ԋʂU ē F ̋ ʂł Ȃ Ƃ C Ⴆ Β Ɉʒu ɒu ʂ Œ肵 悤 ɂ ǂ̋ʂ̘b Ȃ̂ ܂ ܂ ̂ŁC R ̐ ʂ̔z u l ܂ D(1) ʂR i3 A Łj ݂ ɗׂ荇 Ă ꍇ P ʂ D ԋʂ͎c ̏ꏊ Ɏ I ɓ D(2) ʂQ ݂ ɗׂ荇 C P ̐ ʂ ɐ 2 ځC3 ځC4 ځC C6 ڂɂ ꍇ 4 ʂ D ԋʂ͎c ̏ꏊ Ɏ I ɓ D(3) ǂ̐ ʂ ׂ荇 Ȃ 例題(11)6人を部屋a、b、cに分ける場合の数を求めよ。但し空室があっても良いものとする。 場合の数と確率の分野では、原則として「人」は何も書いていない場合は区別します。 一人一人が3つの部屋の内から行きたい部屋を選ぶと考えて、3 6 =729(通り)//



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾



場合の数の一般問題 京極一樹の数学塾



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス
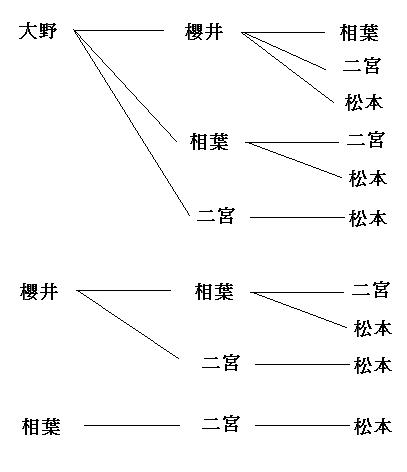



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




場合の数 2 作業性の特訓 書き上げて解く組み合わせ 思考力算数練習張シリーズ 24 エム アクセス 本 通販 Amazon
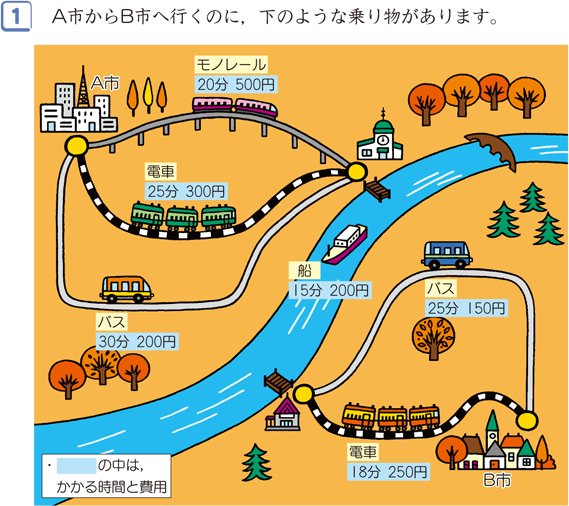



場合の数 算数用語集




数学a 場合の数 組み合わせの総数 Youtube
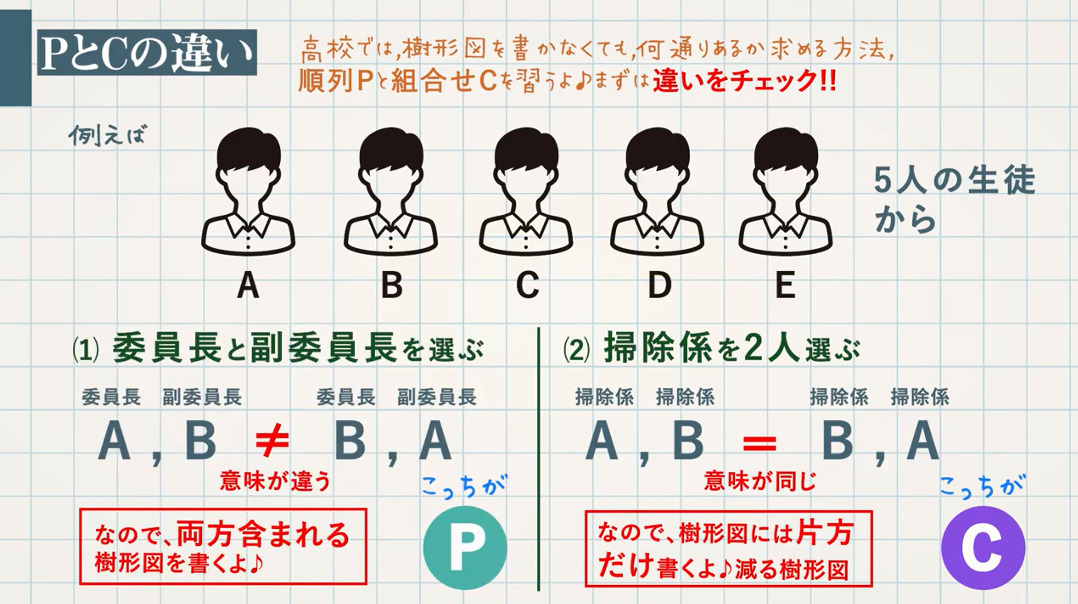



場合の数 番外編 順列p 組合せc 教遊者




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




中学数学 場合の数




これならわかる 図解 場合の数と確率 佐藤敏明 本 通販 Amazon
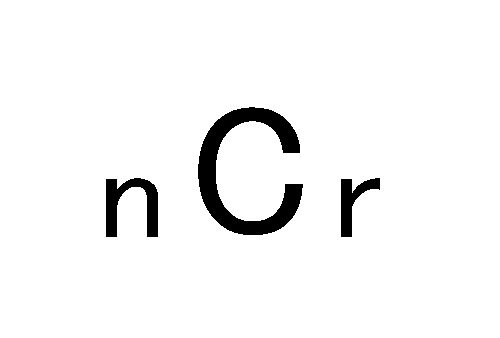



組み合わせの基本と計算方法 順列との違いを説明 統計学が わかった



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾



計算するから難しい 小学生の場合の数は 数え方 が大事 みけねこ小学校




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




6年算数場合の数 1 教え方のポイント



場合の数 算数用語集




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス




場合の数 組み合わせの計算方法について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




公式集 4 3 場合の数 組合せ 分ける 編 コメディカル受験対策講座



場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




場合の数 無料で使える中学学習プリント




場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します




場合の数38 重複組合せの導入3 怜悧玲瓏 高校数学を天空から俯瞰する



1



小学校で扱う場合の数の組み合わせの考え方 みけねこ小学校




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




スマホok 6年 並べ方と組み合わせ方 場合の数 並べ方を考えよう Youtube



数学 確率を極めるには 場合の数 を極めろ




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列の問題 一定の条件で並べる 高校数学の知識庫



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾



順列と組み合わせ 算数用語集




中学数学 場合の数



中学受験 場合の数の問題 解き方の総まとめ 数字カード 道順 色分け等 そうちゃ式 受験算数 新1号館 数論 特殊算



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b



場合の数 順列と組み合わせの違いと並べ方問題の解き方




高校数学a 組合せとは 映像授業のtry It トライイット




場合の数 並べる と 選ぶ の計算方法の違い




高校数学a 組合せの活用1 点を結ぶ 例題編 映像授業のtry It トライイット




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



1




順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート




中学受験 算数 場合の数 入門編 順列と組み合わせの違い Youtube




苦手でも分かる 順列 P と組み合わせ C の使い分け 確率 ともよし塾 受験と科学の解説授業




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



順列 組合せの場合の数と確率の例題 Of 京極一樹の数学塾




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




順列pと組み合わせcの違いと 簡単 な見分け方



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典



1




順列と組み合わせの公式とその違い 問題付き 理系ラボ




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




場合の数 組合せについて 日々是鍛錬 ひびこれたんれん



1




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




場合の数 並べる と 選ぶ の計算方法の違い




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



樹形図の書き方のコツと注意点 中学受験で 場合の数 をマスターする 中学受験ナビ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




高校数学a Npr と Ncr の使い分け 映像授業のtry It トライイット



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




1 順列と組み合わせについて 数学帝國への逆襲 西春自習質問教室のブログ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




高校 数学a 場合の数24 組合せの計算 15分 Youtube




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




重複組み合わせ は2パターンを区別すればok



場合の数とは コトバンク




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ
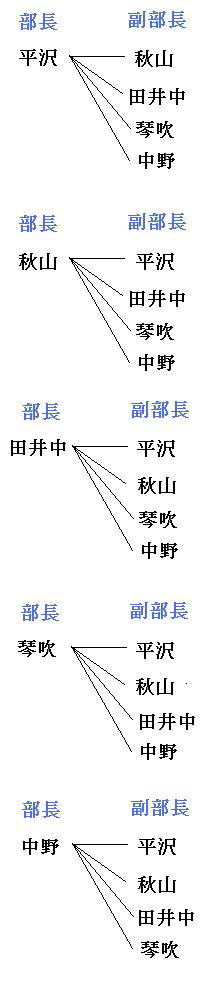



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




場合の数 並べる と 選ぶ の計算方法の違い




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




場合の数 順列 と 組合せ の 違いを例題付きで解説します




順列と組み合わせ 算数用語集



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月



0 件のコメント:
コメントを投稿