テイラー展開が可能であるためには、 f(x0) はもちろん、任意の階数の微係数 d dxf(x0), d2 dx2f(x0), ⋯ が全て計算できる場所でなくてはいけない。 たとえば、 f(x) = √x を原点 x = 0 の回りにテイラー展開することはできない(つまり、この関数は原点においてこちらを二項定理を使って展開をしていくと、 一般項は次のような形になり、 になるための の値を見つけることができます。 になることが分かれば、一般項にあてはめて計算をしていきましょう。 よって、 の係数は であることが求まりました。 答え平方根の展開 √ x は他の個所でも扱っているが、ここでは別の方法で展開する。 以下は 0
パラメトロン計算機 平方根の連分数展開
平方根 展開
平方根 展開-と置いてみる(展開可能性は認めてしまうので、以下は証明ではない)。両辺に1 x をかけると 1 = (1 x)(a0 a1x a2x2 a3x3 O(x4) = a0 (a1 a0)x (a2 a1)x2 (a3 a2)x3 O(x4) 左辺はx を含まないので、x の各次の係数がそれぞれ0 となり a0 = 1;a1 = a0 = 1;a2 = a1 = 1;a3 = a2 = 1 もっとも、これが微分するよりも根号を含む式の展開 さて、根号は文字と同じ、と書きましたが、これは式の展開にもいえます。 例題 () を展開しなさい。 a (b c)=ab ac という、分配法則を用いて計算します。




根号4的算术平方根是多少48的平方根等于多少48的平方根和算术平方根为多少
連分数展開という、ちょっとおもしろい計算があります。 こんな感じです。規則的な連分数展開として、最も有名なのは黄金比 (1√5)/2 でしょう。 * なぜ黄金比は美しいのか >> didrikunora 平方根の連分数展開は、規則的に一定の周期を繰り返すということが知られ展開の公式があと \(2\) つありました。 それ対応する因数分解が当然 \(2\) つあります。 まずは平方の公式です。 \(x^22axa^2=(xa)^2\) \(x^22axa^2=(xa)^2\) 例題1 次の式を因数分解しなさい。 \(x^28x16\) 解説 まずは前回習得した方法で因数分解をしてみましょう。なぜ上のような展開式になるのかの解説はない。私は、ここでつまずいた。 しかも、この後、2項定理や三角関数の級数展開へと話が急展開する。とても追いつかない。そこで、平方根のところで立ち止まることにした。 1 平方根算出のための級数展開
11D例題03雙重根號的化簡 上傳學習單 下載學習單 你喜歡這支影片嗎? 快來幫這支影片打分數吧! 你不喜歡的原因是? 影片教的聽不懂 影片教得很無聊 聲音讓人想睡覺Ascii (object) ¶ 与 repr() 类似,返回一个包含对象的可打印表示形式的字符串,但是使用 \x 、 \u 和 \U 对 repr() 返回的字符串中非 ASCII 编码的字符进行转义。 生成的字符串和 Python 2 的 repr() 返回的结果相似。 bin (x) ¶ 将一个整数转变为一个前缀为"0b"的二进制字符串。结果是一个合法的 Python 表达 今回は平方根の計算を学ぶ。 定期テストレベルでは、今回までの内容ができれば、 平方根の分野で平均点以上を取れる。 公立高校入試では、大問1の小問集合などでよく出るので、 確実に得点できるようにしておこう。 前回 ←平方根の計算の準備(基) 次回 →平方根の計算(標)
授業実践記録(数学) 全国の先生方による工夫された数学の授業実践を「授業実践記録」として紹介します。 なお,以前に紹介していました「課題学習の指導」 (1998年4月~05年3月)と「実践記録」 (1998年4月~1999年2月)もここにまとめました。 19年1月動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



标准差的样本计算公式展开 标准差的简单计算公式 计算公式




機器學習數學筆記 Taylor展開式與擬牛頓 碼上快樂
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaruまずx の関数f(x) に対するTaylor 展開の公式を導出しよう。*1Taylor 展開は任意のx = a の 近傍で関数を級数に展開するものだが、実はx = 0 の近傍で展開できれば話は充分である。これは 特にMaclaurin 展開とも呼ばれる。f(x) はx = 0 で何度でも微分可能であるものと和と差の積 こいつらは平方根の計算式につかってもOK。 むしろ、ガンガン使って欲しいね。 今日は、 3つの展開公式を使った平方根の計算問題 をといていこう! =もくじ= 展開公式を



1




泰勒展開式計算平方根 Lexra Pixnet 痞客邦 泰勒展開式程式
コラム テーラー展開(難易度1) 多くの関数f (x)は、abxcx 2 dx 3 ex 4 のような級数の形に展開することができます。 (この級数が収束する範囲内で) 例えば三角関数 sin x は のような無限級数となり、これはsin xのテーラー展開と呼ばれます。 関数f (x テイラー展開による証明 一般化二項定理の証明にはマクローリン展開( x = 0 x=0 x = 0 でのテイラー展開)を用います。 α \alpha α が非負整数の場合にはただの二項定理です。それ以外の場合(有限和で打ち切られない場合)も考えます。 x > 0 x>0 x > 0 の場合31 平方根 我們知道每一個正數a都有兩個平方根,其中正的平方根記作「」,讀作「二次根號a」,並簡稱為「根號a」;而負的平方根記作「」,例如:4的平方根記作,即=2及=2。當a=0時,a的兩個平方根都為0。在這裡,a稱為 被開方數 。




根号4的算术平方根是多少48的平方根等于多少48的平方根和算术平方根为多少




二项式定理 维基百科 自由的百科全书
展開して整理する 左右を比較し よって、 ・・・答 (4) 展開して整理しよう。 左右を比較すると これを、普通に連立しようとすると、難しい 今回, a,bは整数なので整数問題の知識で解こう。 正の整数a, bを掛けて6になるということは逆数と平方根を求める高次収束アルゴリズム 細田 隆之 09年11月16日 ニュートン法(NewtonRaphson methode)は関数 f(x) を近似値 x n のまわりで1次近似したものであるが、 高次の近似により収束速度を高めることができる。 English edition is hereNote 有理数の連分数展開は必ず有限で終了することが知られている。 平方根の連分数展開 方針は同じであるが、平方根の場合は、適当に分母を有理化することで、整数部分を計算することができる。 例1 $ \sqrt{2} $ の連分数展開。




根号4的算术平方根是多少48的平方根等于多少48的平方根和算术平方根为多少




平方根练习题 Doc 文档分享网
式の展開乗法公式を1瞬でマスターできる3つの覚え方 中2数学 19 一次関数テストに出やすい!平行な直線の式の求め方 中3数学 二等辺三角形の底辺の長さの求め方がわかる3ステップ 中3数学 3秒で計算!平方根のおよその値 (近似値) 解説動画 ≫ 5 =224, 50 =707とするとき,つぎの値を求めよ。 500 5000 05 45 5 4 5 500 = 100 × 5 = 10 5 5 =224 を代入 10 5 = 10×224 =224 √の中を整理して 数× 5 の形にする 5000 = 100 × 50 = 10 50ルート2が無理数であることの4通りの証明 レベル ★ 入試対策 式の計算 更新日時 2 \sqrt {2} 2 は無理数である。 より一般に,平方数でない正の整数




平方口诀表11 100平方根口诀表 附100以内的平方数




平方根 式を展開する 苦手な数学を簡単に
次の文が正しければ 、間違っていれば×を書きなさい。 (1) 9 の平方根は 3 だけである。 (2) 001 の平方根は 01 と01 である。 (3)x2の平方根は x である。 (4) –25 の平方根は存在しない (5) 0 の平方根は 0 だけである。 解説ページに解説がない問題で、解説導入を工夫する 利用の手引き 山口県中学校数学教育会「数学指導ハンドブック第2集」より 学年 単 元 内 容 1年 整数の性質中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 √の中が等しい数は、文字式の同類項と同じように分配法則を使ってまとめることができることなどについて理解し、平方根の加法・減法を練習する問題プリントです。



Http 163 23 69 2 Rjt Public E6 95 99 E5 Ad B8 E7 B5 84 E6 Ad E5 B1 86 E6 Ae B5 E8 80 E8 A6 E9 A1 8c 103 E5 Ad B8 E5 B9 B4 E5 Ba A6 E4 B8 8a E5 Ad B8 E6 9c 9f E7 Ac Ac1 E6 Ac A1 E6 Ae B5 E8 80 E6 95 B Pdf



初中数学求算术平方根 有人秒出答案 有人无从下手 原因在这儿
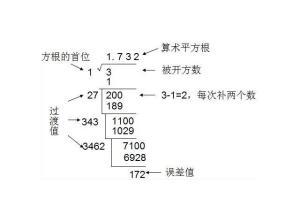
102 ニュートン法から得られる平方根,立方根,4乗根の連分数表示 定理3 連分数表示の漸化式 は,平方根 ±√a を求める式である. (2.1.7)の分母に(1.2)の右辺の漸化式があることに注意せよ.第3学年で学習する単元一覧 ※啓林館の教科書に対応した授業展開案です。 ★ マークの学習内容については、詳細な授業展開案(pdf)も用意しています。より詳しい解説を知りたい方は、それぞれの計算について別記事を用意していますので、そちらを先に読んでみて下さい。 加法: 中3数学根を含む加法の解き方とは? 同類項同士で計算する方法について解説します! 減法: 乗法: 中3数学平方



初中数学 求平方根问题不会做 总出错 一节课帮你搞定




要点 展開の公式と平方根の計算 Youtube
展開の工夫で学んだ方法を利用していく。→展開の工夫 (1) 同じ部分をaとおく (2) マイナス1でくくって同じ部分をaとおく (3)(4) 一部の項をまとめて考える (1) 同じ部分をaとおけば、計算が楽になるのだった。 よって、 とおく




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく



パラメトロン計算機 平方根の連分数展開




詹森不等式 注意詹森差距 Weixin 的博客 Csdn博客




泰勒展開式計算平方根 Lexra Pixnet 痞客邦




2的算術平方根 維基百科 自由的百科全書




Ukf If



Arctanx的泰勒展开式 西瓜视频搜索



开方公式 万图壁纸网



九年级数学下册第3章三视图与表面展开图3 4简单几何体的表面展开 图作业设计 含解析浙教版 文件编号 初中数学 学习资料大全 免费学习资源下载




泰勒级数展开 程序员宅基地




ルートの展開 展開公式と同じ解き方で計算しよう 中学や高校の数学の計算問題



立方根换算 算术平方根 平方根与立方根的区别与联系 尚书坊



完全平方根公式 平方根怎么算出来 学习岛



中考数学审题的常用策略 腾讯新闻



平方根公式怎么算 如何计算平方根 学习岛
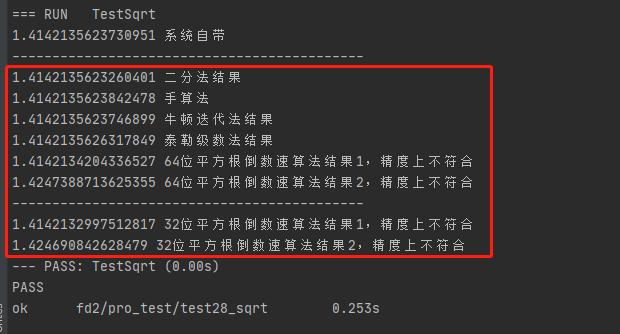



C语言迭代法求平方根 07 28 已知sqrt 2 约等于1 414 要求不用数学库 求s Juicymio的博客 程序员宅基地 程序员宅基地



3



1




一般的一元二次方程的解法 直接开平方法 因式分解法 知识讲解 快资讯
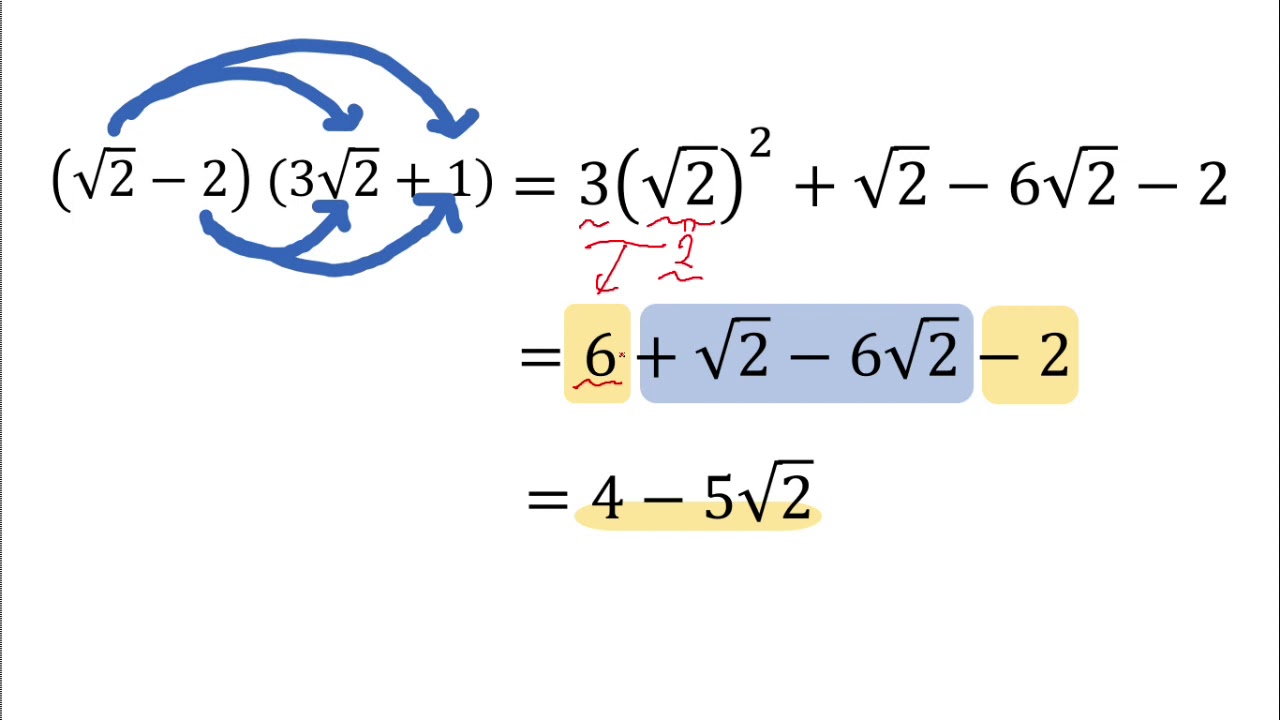



中3数学 ルートを含む式の展開のやり方を解説 Youtube




多元函数的泰勒展开式 Allenlzcoder的博客 程序员宅基地 多元函数泰勒公式 程序员宅基地




一点五的平方根化简 100以内的根号表 二次根式化简的基本方法



开平方 搜狗百科



平方根计算 搜狗百科



广义二项式定理展开式 广义二项式公式 牛顿二项公式展开式



0 01是谁的平方根 0 81平方根 几的算术平方根为0 01




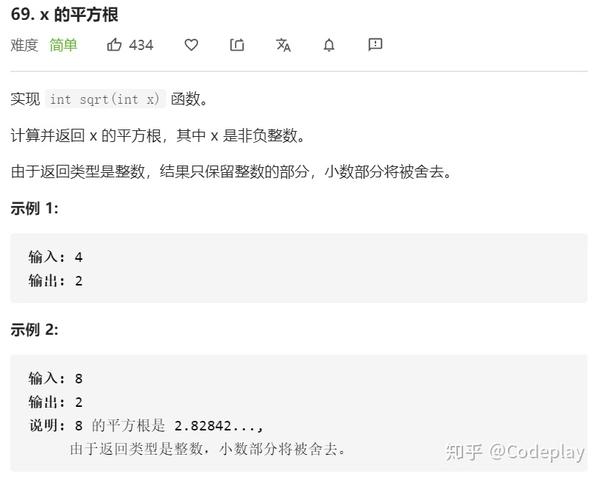
Leetcode X的平方根 M1ng



13 8 快速平方根和平方计算 1 51cto Com




X的平方根的golang实现 华为云




0 81的平方根是什么 过程 49的平方根等于多少 7的平方根



精选二四六天天好彩头 蓝月亮二四六精选大全 二四六好图片玄机图小说




例題 展開の公式と平方根の計算 Youtube




Leetcode X的平方根 M1ng



学霸在线 初中平方根 算数平方根和立方根详解 哔哩哔哩 Bilibili



S9ujsaqljewzjm




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく



中学数学なら数学わかルート 無料動画で学ぶ



Arctanx的泰勒展开式 西瓜视频搜索




微博搜索



算子平方根的holstein Primakoff展开和微分方程方法的恢复 Physical Review Research X Mol




平方根 搜狗百科




算术平方根 1445的近似计算 百度经验




蚂蚁算数 6 12 开平方根 知乎




大学高数题不会可以用什么软件搜题 大学题不会用什么软件 精作网



根号五怎么算过程 平方根口诀表 五的平方根计算过程




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく



139 5的平方根 0 0032的平方根 0 75的平方根




泰勒展開式計算平方根 Lexra Pixnet 痞客邦 泰勒展開式程式




Ckadfwa9kecgrm




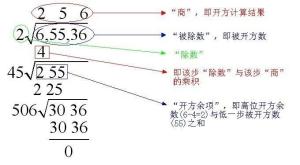
手算开平方 知乎



手算平方根的正确方法 Li Hua 博客园



初中数学 理解了平方根和算术平方根 这些提高题做起来很简单




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




0的算术平方根是多少0 0025的算术平方根0 0025的算术平方根等于多少




平方根 數學符號 平方根 又叫二次方根 表示為 其中屬於非負數 百科知識中文網




平方根练习题 Doc 文档分享网




4d數學第四課 兩邊取平方根解二次方程 Youtube



初中数学 平方根知识点题型归纳 别以为简单 很多同学都不会 哔哩哔哩 Bilibili



立方根换算 算术平方根 平方根与立方根的区别与联系 尚书坊




开方算法 知乎




牛顿 拉夫逊简单解释 台部落
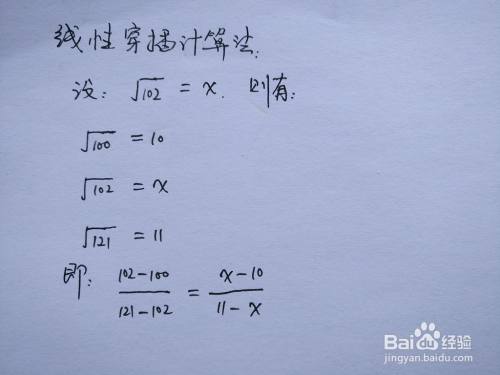



算术平方根 102的近似计算 百度经验




求解平方根 Matrix Csdn博客



平方根公式表100以内 初中数学100以内的平方数公式表 学习岛



平方根定义 立方根的定义平方根的定义 尚书坊




初中数学最全运算法则 实数 平方根 立方根 整式 分式运算律 中考



如何学好初一下册算术平方根 看老师的总结刷题 附答案可打印 樊正伟



36的平方根是什么 西瓜视频搜索



Www Cnblogs Com Xkfz007 Archive 12 05 15 Html



班主任推荐 初中数学知识全归纳 打印版 用过都说好 小初高题库试卷课件教案网



1




机器学习数学 Taylor展开式与拟牛顿




平方根解法配方法解一元二次方程式一元二次方程式的公式解 Ppt Download




觀念 利用平方根概念解一元二次方程式 Youtube



2的平方根怎么算图解 图片欣赏中心 急不急图文 Jpjww Com



二次平方根公式 二次平方根的运算依据什么 学习岛



解平方根 快懂百科
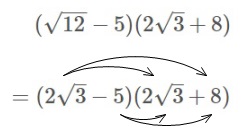



展開公式を利用するルートのついた無理数の計算問題とポイント



平方根 立方根 我的网站




機器學習數學筆記 Taylor展開式與擬牛頓 碼上快樂




计算机 负一的平方根




平方根计算器app下载 平方根计算器软件下载 V0 19 计算器下载站



平方根の連分数展開




算术平方根 1445的近似计算 百度经验




如何3秒钟判断一个大平方数的平方根 假装的最强大脑课




平方根 二 演示文稿下载 Ppt模板 爱问共享资料



手算平方根的正确方法 Li Hua 博客园




泰勒展開式計算平方根 Lexra Pixnet 痞客邦 泰勒展開式程式
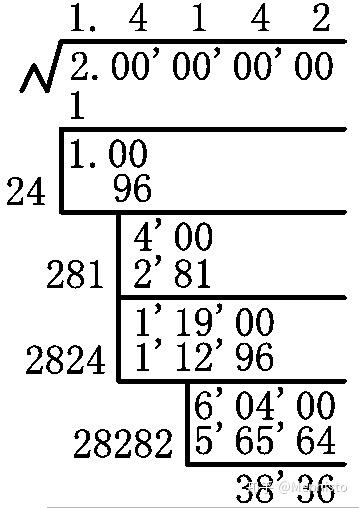



开方算法 知乎




計算某數平方根的公式和疊代公式 每日頭條



0 件のコメント:
コメントを投稿