工夫していろいろな角度を求める問題で、平行線の錯角や同位角が等しい性質、三角形の角の性質を使う問題です。 よく出る問題で練習してから応用問題に取り組んでいくようにしましょう。 平行線の角度の性質を使った問題 例)矢印のつ入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺大人のための算数。それが最上級問題です。 算数を極めたい大人の方向けのコーナーです。中学入試の難易度を超えた難問や良問をぜひお楽しみ下さい。 最上級問題 PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 解けた方はお気軽に@sansu_seijin宛に
三角形の角度を求める 思考力を鍛える数学
三角形の角度の問題
三角形の角度の問題-三角形の外角三角形の外角は、これととなり合わない \(2\) つの内角の和と等しい。 また、三角形 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料のオンライン学習ページです。右の図のように, ∠bac=42°, ab=ac の二等辺三角形 abc があり,辺 ac 上に ad=bd となる点 d をとる。 このとき, ∠x の大きさを求めなさい。 (山口県15年入試問題)



角度の求め方 算数の教え上手 学びの場 Com
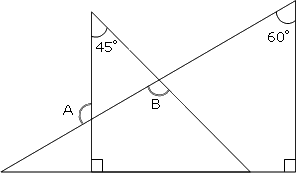
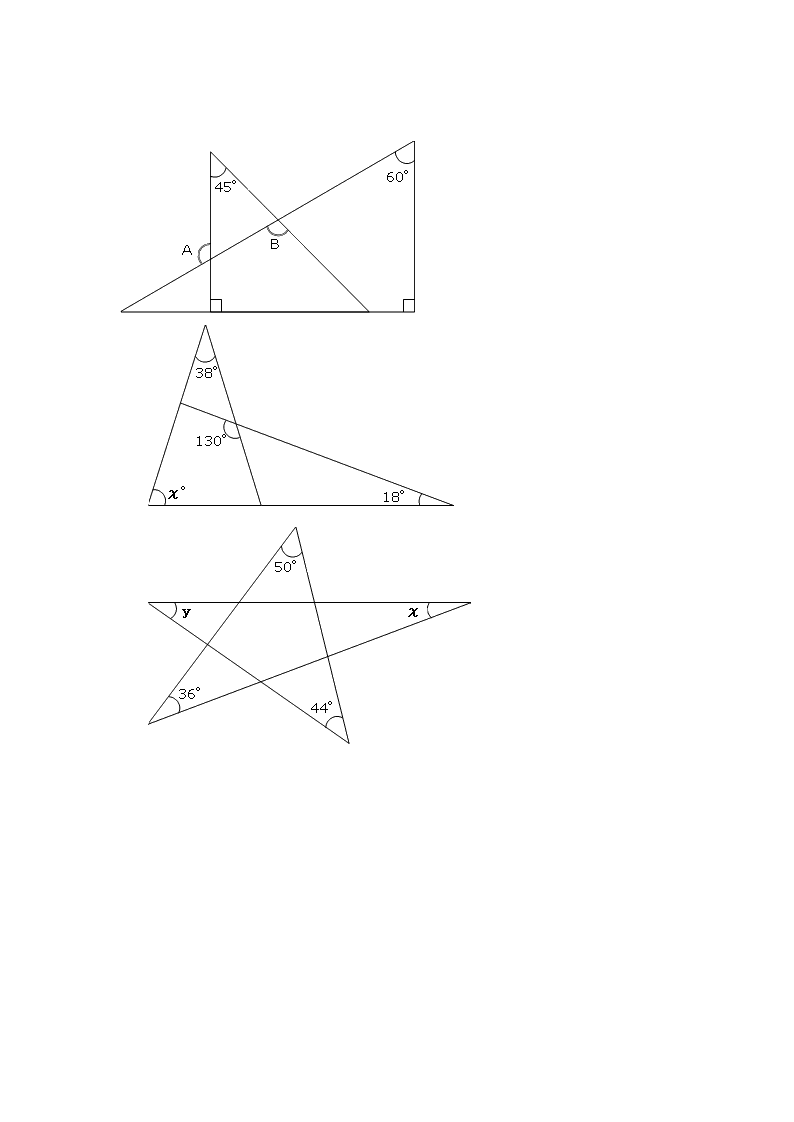
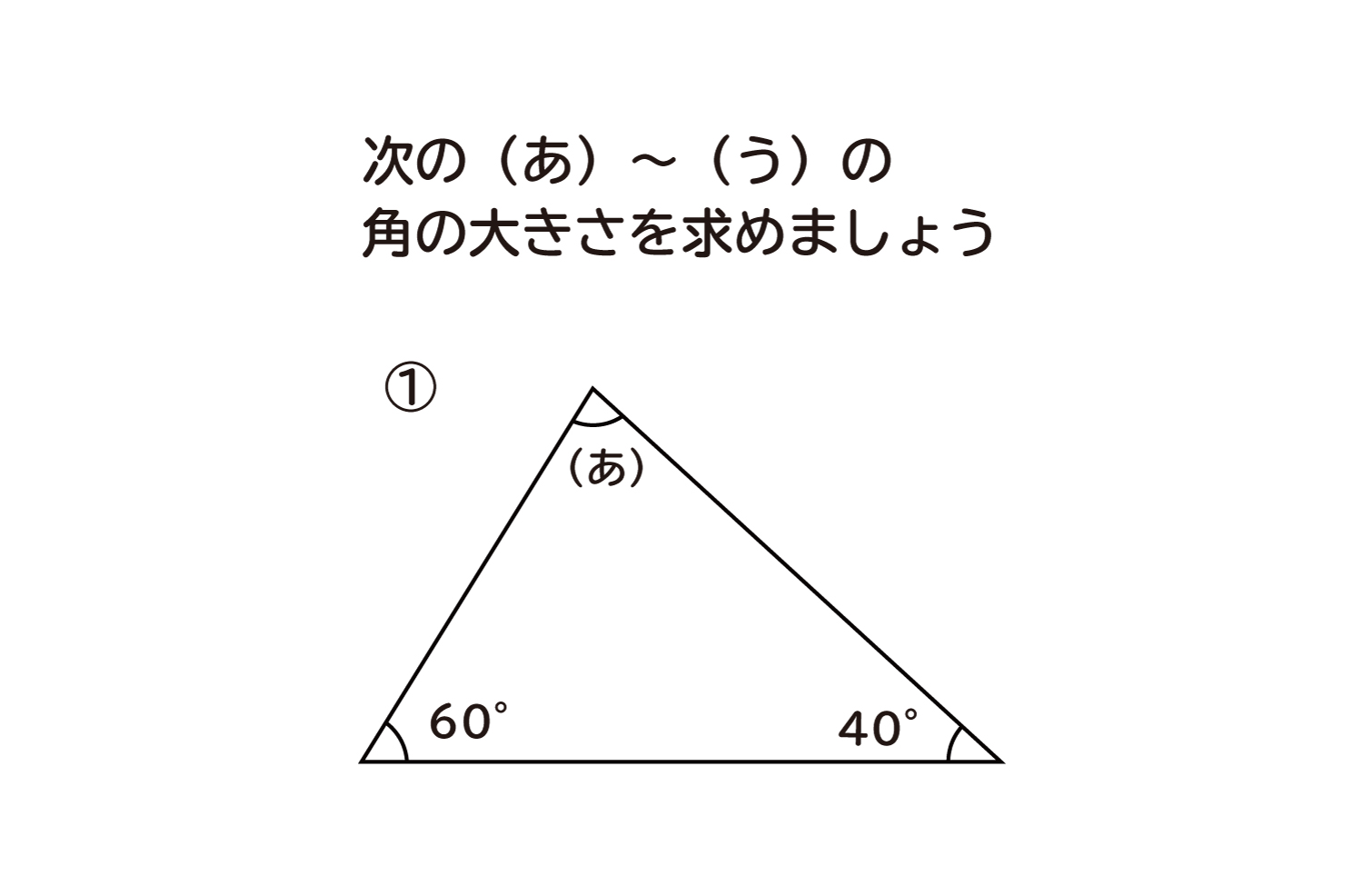
角B=180°-(30°+45°) =180°-75° =105° と計算できます。 この角Aように、あらかじめわかる角度を図に記入して、三角形の内角と外角の関係(三角の旗)を利用すると簡単に正解が得られる問題はたくさんあります。 答え 角A=1°、角B=105°問題(,60、50、30)の答え はX=30ですが、 問題(.60. 50,40)となると、その答えは X=17.9°となり、関数電卓で 逆三角関数を使わないとムリです。 ラングレーの問題 トピックス 整角四角形の解きやすい問題を上から順 に並べています正三角形の角度問題 まとめ お疲れ様でした! 正三角形の性質としては このように単純な性質しかないので 問題としては、いろんな図形との融合で出題されがちです。 正三角形どうしの融合の場合 60°の角になるところをしっかりと見つけていくこと
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な 計算問題も徹底解説 21年2月19日 この記事では、三角関数について、角度の求め方や変換公式( など)について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね! 目次 非表示 三角関数の 三角形の角度を求める問題 ではこれらの性質を使って、三角形の角度を求める問題を解いていきたいと思います。 問題① 下の図における ∠x の大きさを求めなさい。 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135°
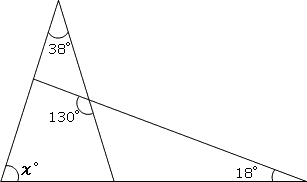
下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 ° 角度③ 応用問題 例題4 1組の三角定規を三角形の内心は、角の二等分線の交点なので、これを利用するといろいろな場所の角度を計算することができます。 例題を解いてみましょう。 例題1: 三角形 ABC の内心を I とする。 ∠A = 70 ∘ であるとき角度 x を求めよ。 解答: 内心の性質より、 BI 皆さん、こんにちは。 今回は、このブログでは珍しい、図形問題を取り上げてみたいと思います。 その名もずばり「ラングレーの問題」。 上の図において、角度xを求めてください、という問題です( ABCは二等辺三角形です)。実は小学生でも解けてしまうので、一度ノーヒントで挑
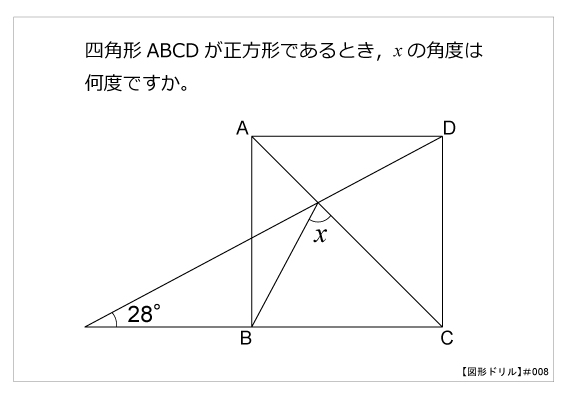



図形ドリル 第8問 正方形と角度 算数星人のweb問題集 中学受験算数の問題に挑戦
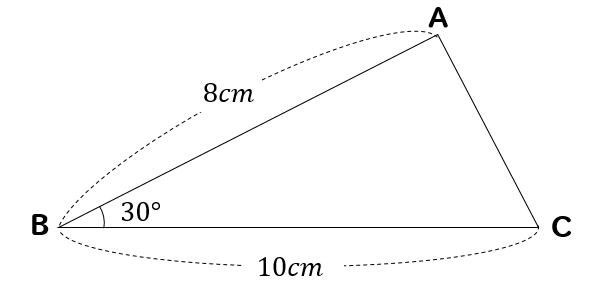



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ
「三角形の内角の和は180°」で、「ぐるっと一周の角度は360°」を忘れないようにして、「平行」にも気をつけながら「角度の関係性」を理解していってほしいと思います。 では、また。 問題pdfはこちら 解答pdfはこちら 三角形の五心⑤ 三角形の傍心とその存在証明 スポンサーリンク 高校数学A 平面図形 検索用コード 三角形の1つの内角の二等分線と他の頂点の外角の二等分線は1点で交わる}}} \\ 2zh その交点を傍心は {1辺と他の2辺の延長からの距離が等しい点 三角形の角度算数プリント 三角定規を使った問題 小学4・5年生で習う三角形の角度計算です 三角定規を使った問題がメインになっています それ以外にも、三角形の角度計算で覚えなければならない決まり事も掲載しています 三角定規の決まり事 角度の
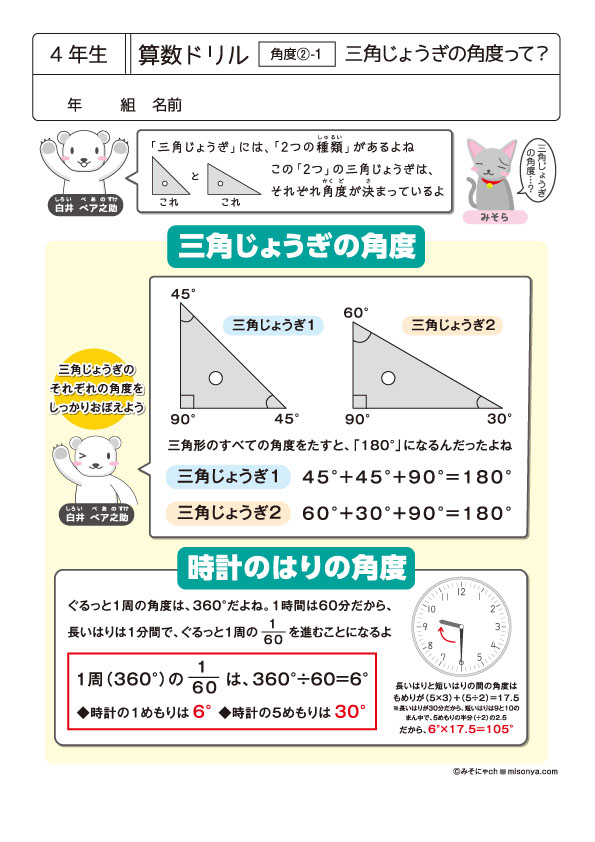



無料の学習プリント 小学4年生の算数ドリル 角度2 三角定規と時計の針 みそにゃch



角度の問題 三角形の内角の和は180 を使って 創造力 問題解決能力を養う
一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 二等辺三角形の2つの底角は等しい. (2) 円周角は中心角の半分になる. 特に, (1)を使って元の角 x 例1)正三角形や正方形を組み合わせた問題 下の図で四角形abcdが正方形、三角形cedが正三角形のときアの角度を求める ce=cdになるので三角形cdeが二等辺三角形になることに着目 ∠cdeを求める よってアの角度h 9075=15° と求めることが出来る。 芸術的な難問 良問数学 中2数学 複雑な多角形 角の和応用問題 今回は複雑な多角形の角の和の問題とその考え方です 星型など複雑な図形の角の和を求めるとき三角形の外角の定理やブーメラン型四角形の角リボン型ちょうちょ型の三角形の角の考え方が役立ちます
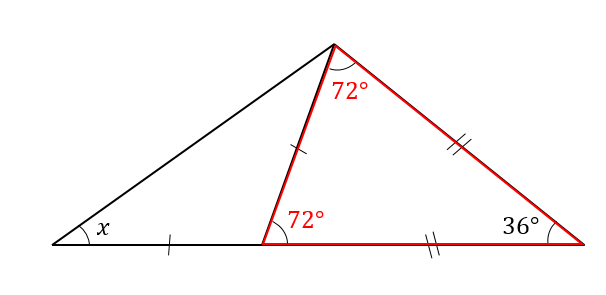



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
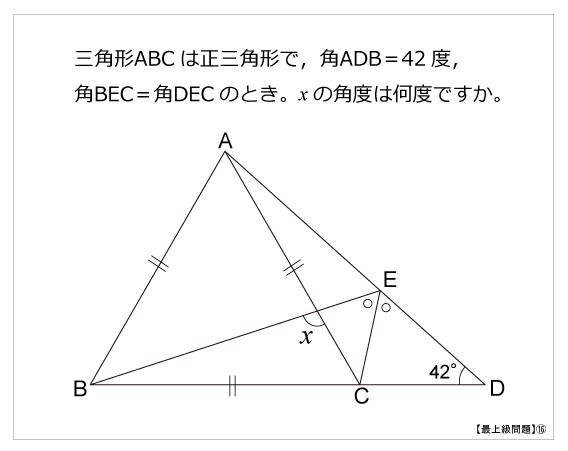



最上級問題 難角問題 算数星人のweb問題集 中学受験算数の問題に挑戦
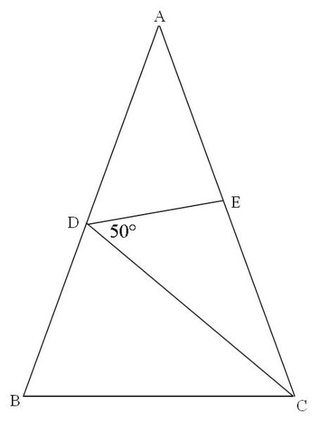
角度の難問 (中学生版) 1 /32 問題 AB=ACの二等辺三角形 ABC があり,角Aは ° です。 いま,辺 AC 上に点D,辺 AB 上に点Eがあり,DからB,EからCに直線を引いたところ,角 DBC = 60° ,角 ECB = 50° となりました。 DからEまで直線を引いたとき,角 BDE (図のχ三角定規を使った問題と良く出る三角形角度の計算編を掲載しています 小学4・5年生で習う三角形の角度計算です 三角定規を使った問題は、4年生がメインとなっています それ以外にも、三角形の角度計算で覚えなければならない決まり事も掲載してい答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を
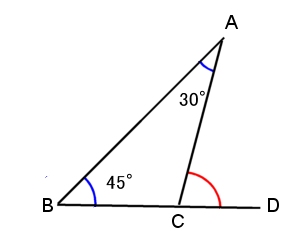



三角形の作る角度1 3



Math 平行と合同 角の二等分線と角度 働きアリ
問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答 求めることができる角度はコレ↓↓ 三角形の外角と内角の関係から、 55°30=∠x よって∠x=85° ・・・(答え) 問題③ こいつも一筋縄ではいかねーな! 右側の三角形で、三角形の外角と内角の関係を利用しよう。 65°45°=110° 次に、左の三角形に着目平行と合同 例題 平行線の錯角・同位角 補助線を引く問題 三角形の内角と外角の関係 印をつけた角の和 角の二等分線と内角の和 三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の




角度の裏ワザ 知ってる人は5秒で解ける中2標準レベルの問題 Youtube



1
114° 三角形の内角の和は 180度だから, 180-62=118(度)イウ ところで,イ =180度, ウ××=180度だから, イウ ××=180+180数学・算数 三角形の角度計算問題 中学や高校ででてくるような三角形の角度計算問題で、どうしても解けなくて困っています。問題の図を言葉で説明しますと・・・ 底辺の長さがdで、残り2辺の長さの比 質問No 三角形の角度を求める問題です。ごく基本的な問題なので、確実に出来るようにしましょう。ポイント 三角形の内角の和は180度 内角と外角はどこか 三角形の1つの外角は、となりあっていない2つの内角の和に等しいこの3つのことを教科書などでしっかり確認してから問題に取り組んでく
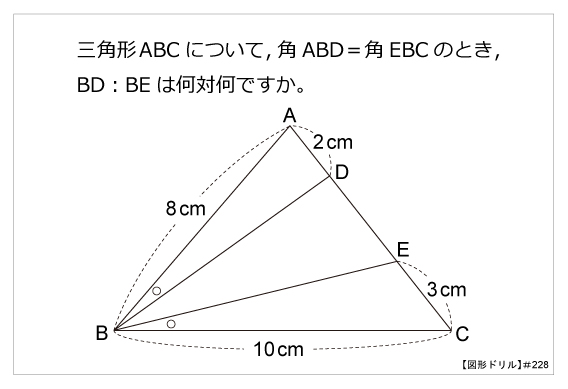



図形ドリル 第228問 等しい角度と辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
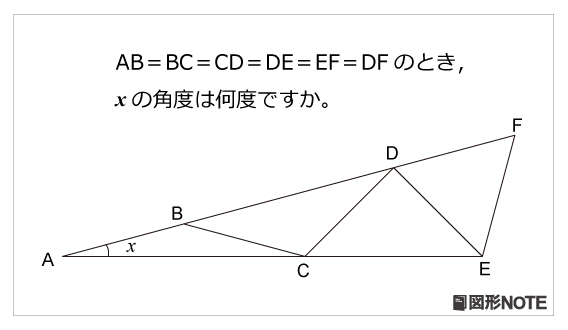



図形noteプレ レベル4 ジグザク角度 算数星人のweb問題集 中学受験算数の問題に挑戦
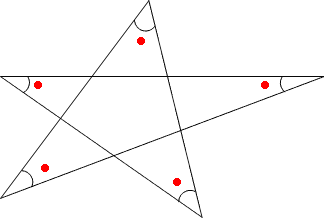
第1問-連続する二等辺三角形 以下の直角三角形において、 x x は何度か 解説 第2問-解けそうで解けない超絶難問 以下のAC=BCの二等辺三角形において、 x x は何度か 解説 まとめ はかせちゃん 1問目が解けたら凄いです。小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。今日は、星型 角形の角度について,紹介します。 まずは,問題に挑戦してみてください! 図の5つの角度ア~オの和を求めなさい。 となります。 図の7つの角度ア~キの和を求めなさい。 例題のような一筆書きした図形を「 星形五角形 」,「 星形七角形



角度の難問 中学生版
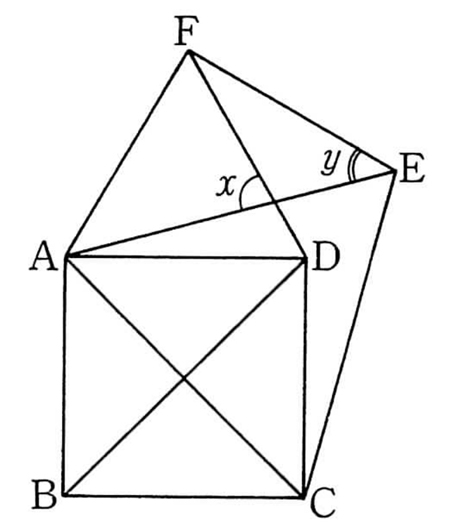



入試に使える算数の基礎 角度の問題
二等辺三角形の角度の問題では 底角が等しいこと 三角形の外角の性質 この2点を覚えておけば応用問題でも解くことができます。 ただし、発想が難しい問題もあるので、いろんな問題集を使って知識を深めておきましょう。 スポンサーリンク三角関数を利用して解決した先輩もいらっしゃ いましたが・・・ 皆さんもちょっとチャレンジしてみて下さい! 1.次の図のような平行四辺形ABCDで、角χの大きさを求めなさい。ラングレーの問題 別名「整角四角形」「フランクリンの凧」 とか呼ばれる問題です。 面積の問題 正方形や正三角形を組み合わせて 面積を求める 等しい長さを持つ三角形 三角形の辺に等しい長さを持つ三 角形で、やはり角度の問題、三角形




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
三角形の角度を求める 問 ABC A B C について, BC B C の中点を D D とすると, ∠DAC = 15°,∠ADB = 45° ∠ D A C = 15 ° , ∠ A D B = 45 ° となった. ∠BAD ∠ B A D を求めよ. 16/8/ 幾何 ★★★☆☆ hide or visible




余弦定理で角度を求める方法 数学の星




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



工夫しないととても難しい角度問題 横須賀学院中学 11年 どう解く 中学受験算数



二等辺三角形の頂角を求める問題 難問 東大合格コム



円と三角形 角度 中学から数学だいすき




三角形の角度を求める問題 小学生 中学生の勉強



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル



ラングレーの問題 整角四角形



幾何大王からの挑戦状 角度の問題 12



角度の問題 Part6



図形の調べ方 角度を求める問題 苦手な数学を簡単に



Studydoctor多角形の角度の問題 中2数学 Studydoctor
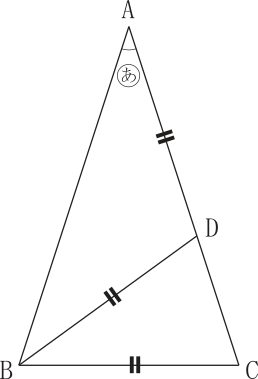



二等辺三角形 In 二等辺三角形 角度の問題 算数の広場




算数の問題でもあり 数学の問題でもありますの解答解説1 角度を求める問題7月19日出題 Fitのひろば
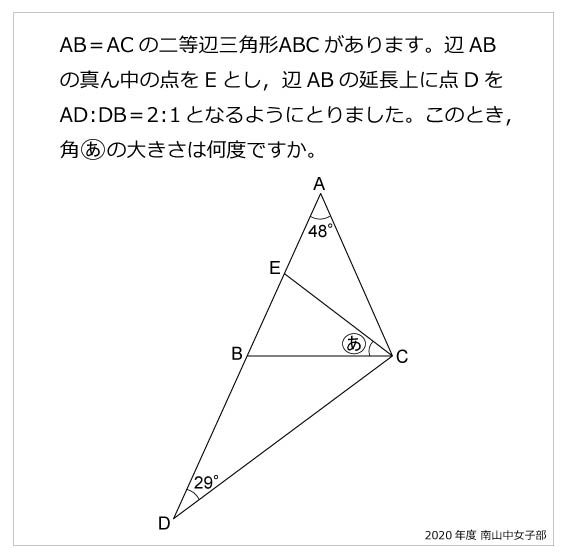



角度 算数星人のweb問題集 中学受験算数の問題に挑戦
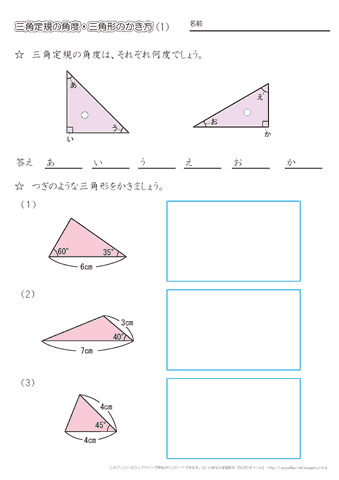



小学4年生の算数 三角定規の角度 分度器を使った三角形のかき方 ちびむすドリル 小学生



中学生の数学 角度の問題



三角形の角度を求める問題がわかりません 三角形の和と直線の角度 Yahoo 知恵袋



1



ラングレーの問題 整角四角形




中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー
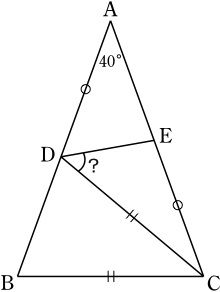



二等辺三角形の頂角を求める問題の 逆 の問題 東大合格コム
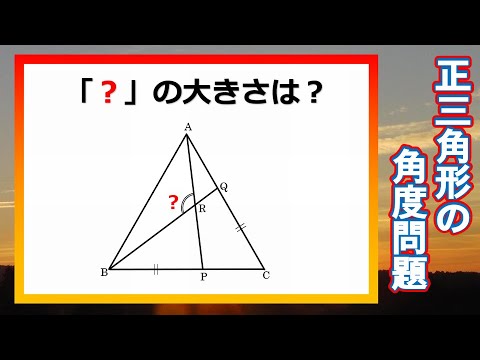



正三角形の角度問題 シンプルですが面白い 脳トレにはちょうど良い問題です Youtube




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
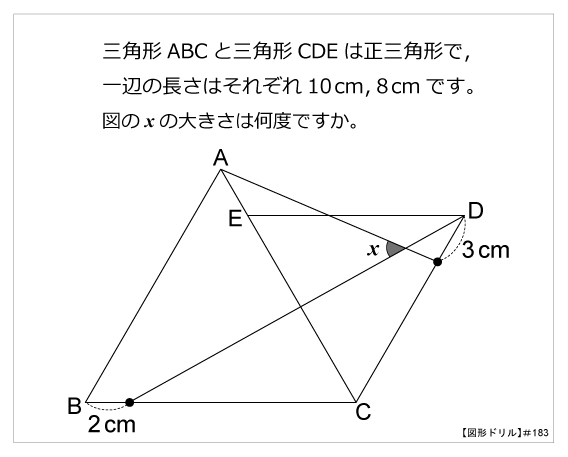



図形ドリル 第1問 正三角形の角度 算数星人のweb問題集 中学受験算数の問題に挑戦
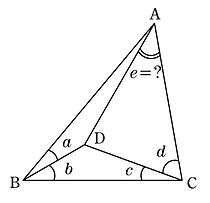



ラングレーの問題 Wikipedia




三角形の角度 無料で使える中学学習プリント
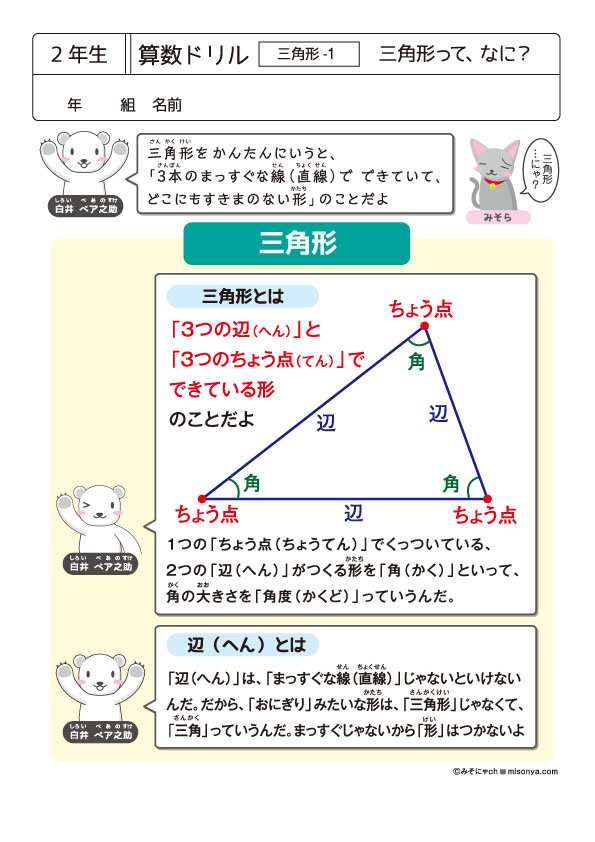



無料の学習プリント 小学2年生の算数ドリル 三角形 みそにゃch



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




重なり合う三角定規を使った角度の計算問題 小4 小5の算数 きいとこ



2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




角度の求め方 算数の教え上手 学びの場 Com
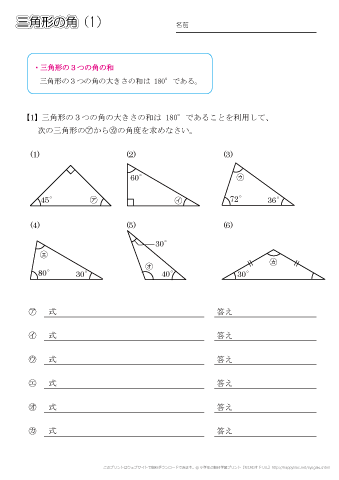



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




算数図形編 角度 三角形の外角の性質を使いこなそう 中学受験 高校受験パスナビ




高校数学a 三角形の内心2 実践 例題編 映像授業のtry It トライイット




二等辺三角形の角度 無料で使える中学学習プリント



2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に




角度の求め方 算数の教え上手 学びの場 Com
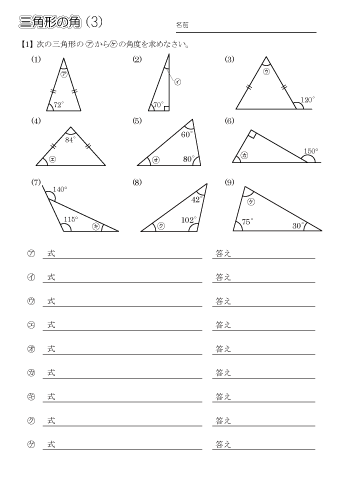



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




小5 算数 小5 31 三角形の角 Youtube




角度の問題まとめ 無料で使える中学学習プリント




中2数学 二等辺三角形の性質1 底角が等しい 練習編 映像授業のtry It トライイット




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト



角度の問題




角度の求め方 算数の教え上手 学びの場 Com




角度計算の難問 特別な三角形を作り出せ 07年算数オリンピック Youtube



角度の求め方 算数の教え上手 学びの場 Com
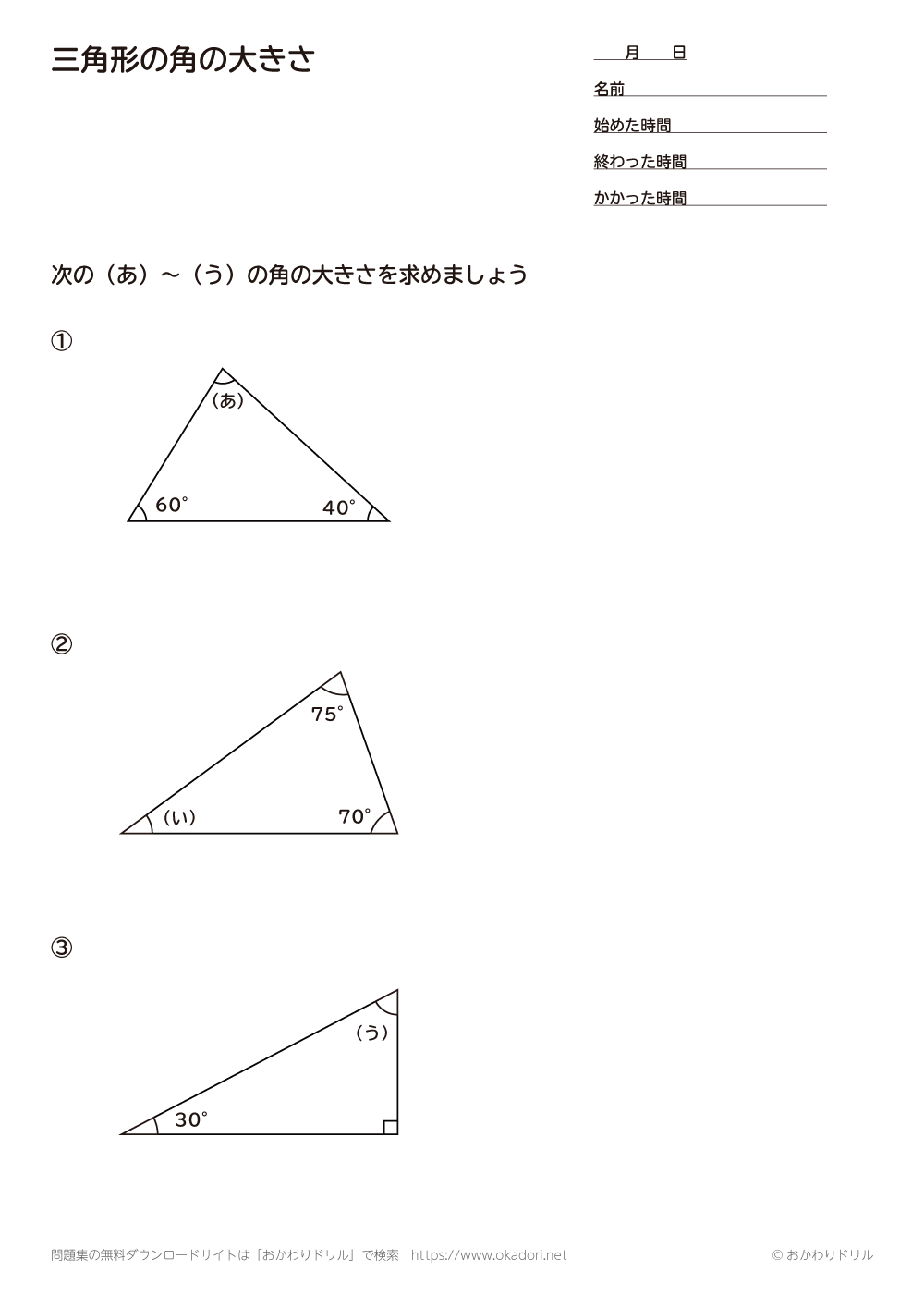



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル
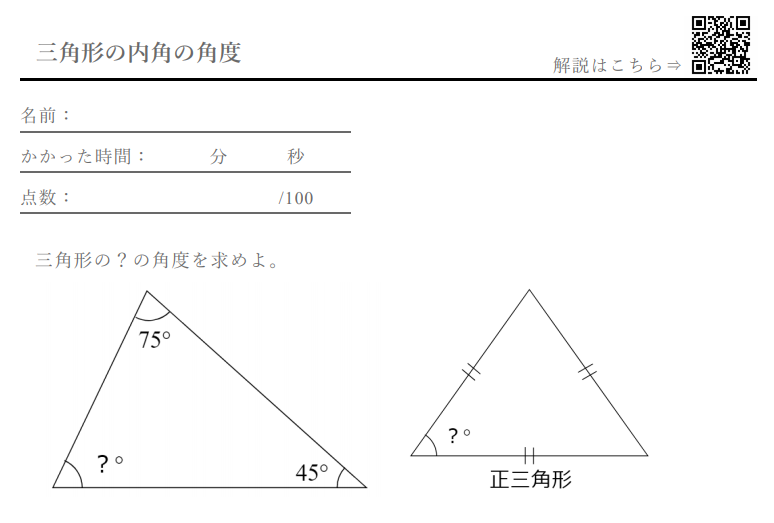



三角形 の内角の角度 計算ドリル 問題集 数学fun
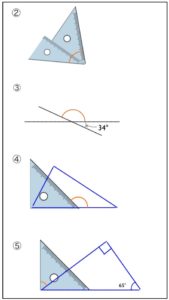



角度の計算 良く出る三角形角度計算編 算数 計算問題プリント 小学5年生 小学4年生
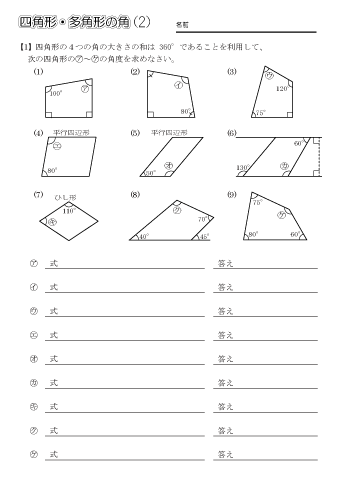



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
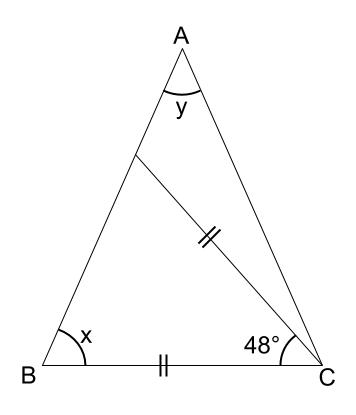



中学数学 二等辺三角形 中学数学の無料オンライン学習サイトchu Su




三角形の角度を求める問題 小学生 中学生の勉強




角度の問題まとめ 無料で使える中学学習プリント
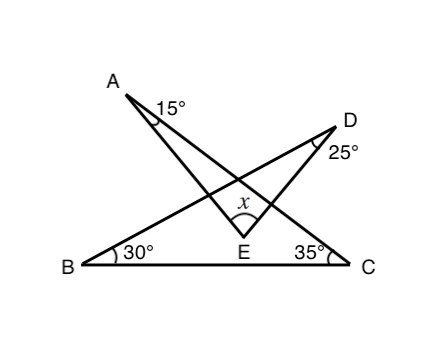



角度を求める問題 スリッパを探そう 苦手な数学を簡単に




中学受験 算数ー角度の問題が分かりません 教えてください 三角形abc 数学 教えて Goo



角度の難問 中学生版
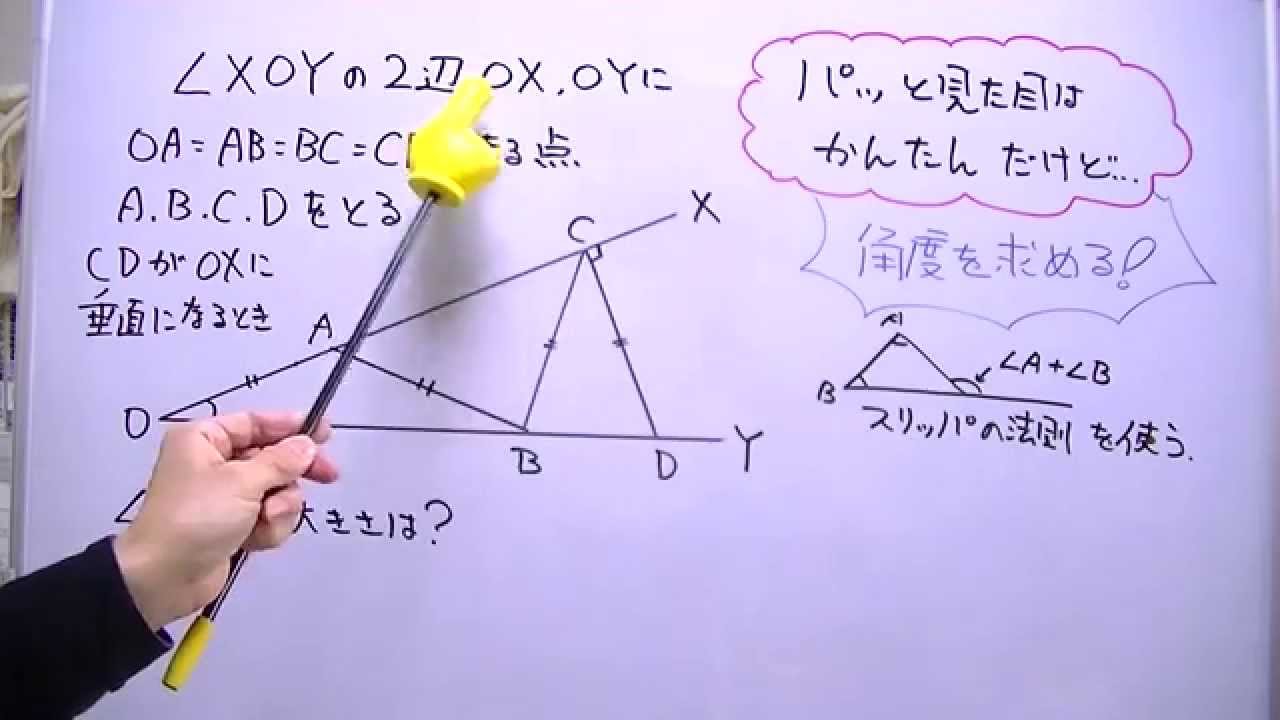



二等辺三角形とスリッパを組み合わせた角度問題 おときち副塾長 電脳空間学習塾かもん Youtube



三角形の角度を求める 思考力を鍛える数学



三角形の角度を求める 思考力を鍛える数学




ラングレーの問題 Youtube



1



図の問題がわかりません 正三角形と正方形を組み合わせた図形で Yahoo 知恵袋
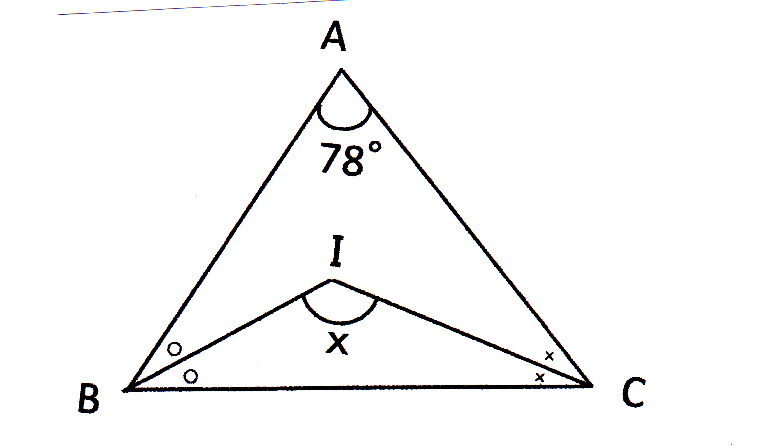



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方



角度の求め方 算数の教え上手 学びの場 Com




角度 図形問題 正三角形を作る 数学難問 高校入試 中2 Youtube




三角形の角度を求める問題 小学生 中学生の勉強




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi




ラングレーの問題 Wikipedia




ラングレーの問題 Wikipedia



角度を求める問題 中学受験 田中貴 Com



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




正三角形の角度問題 シンプルですが面白い 脳トレにはちょうど良い問題です 子供から大人まで動画で脳トレ 楽天ブログ
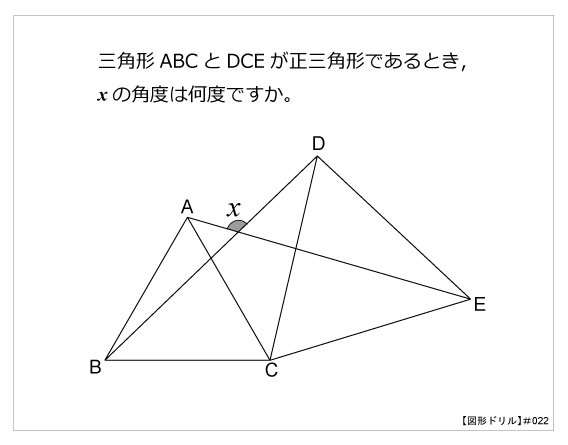



図形ドリル 第22問 正三角形の回転合同 算数星人のweb問題集 中学受験算数の問題に挑戦
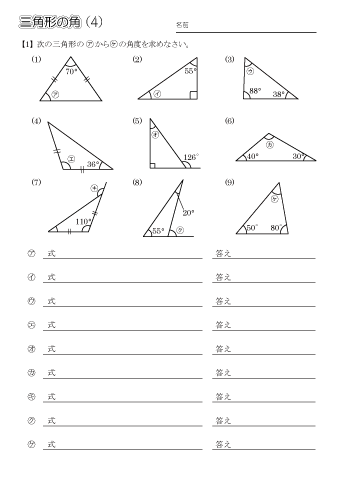



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
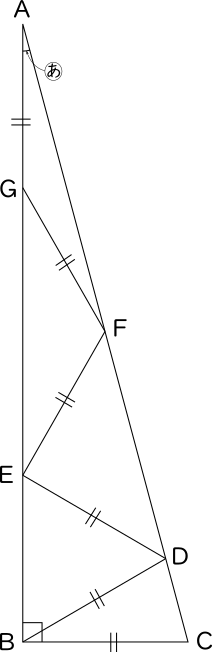



二等辺三角形 In 直角三角形 角度の問題 算数の広場
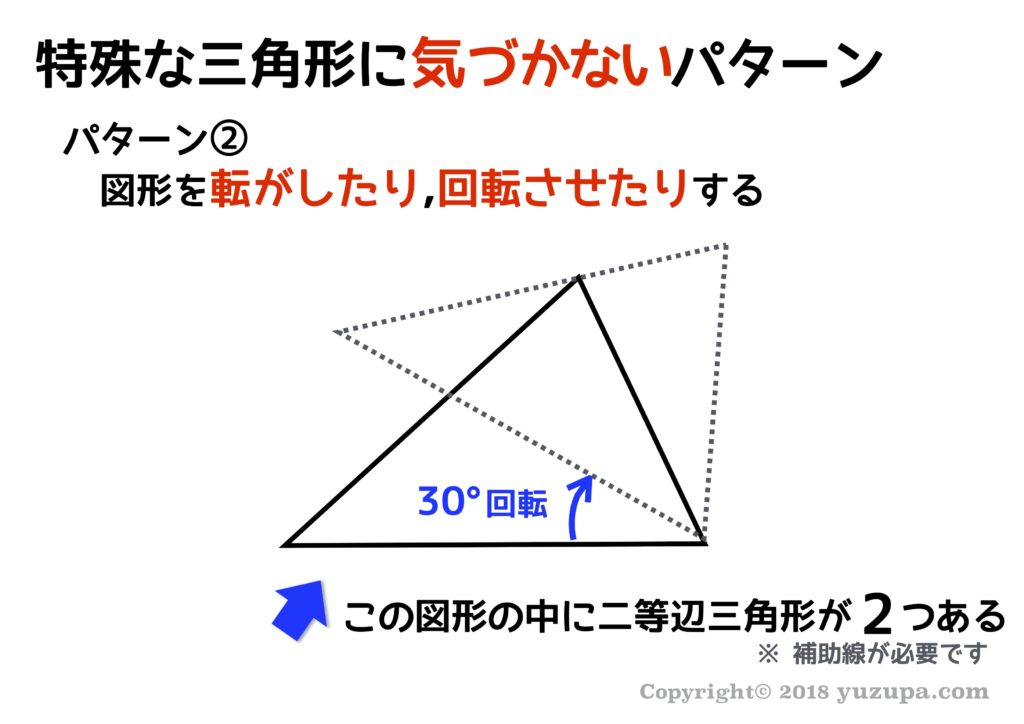



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋



Math 角度の難問 中学2年生 働きアリ
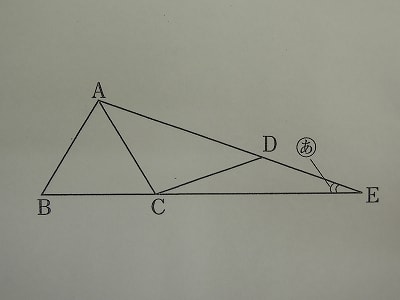



マッキーの一問必答 9 二等辺三角形の性質を利用する問題 1 マッキーのつれづれ日記




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の角度を求める問題 小学生 中学生の勉強



角度問題 第2回算数オリンピック 決勝問題から 算数オリンピック問題に挑戦



1




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



0 件のコメント:
コメントを投稿